题目内容
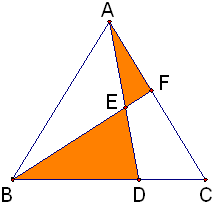 如图三角形ABC的面积是10平方厘米,AE=ED,BD=2DC,则阴影部分的面积是
如图三角形ABC的面积是10平方厘米,AE=ED,BD=2DC,则阴影部分的面积是4
4
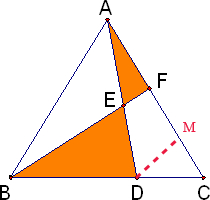
平方厘米.分析:过D作DM‖BF交AC于M(如图)因为BD=2DC,因为AE=DE,所以△ABE的面积与△DBE的面积相等,所以阴影部分的面积为△DBE的面积+△AEF的面积,即三角形AFB的面积,由DM‖BF知道△DMC相似△CBF 所以CM:CF=CD:CB=1:3,即FM=
CF,因为EF是△ADM的中位线,AF=MF,所以AF=
AC,由此即可求出三角形AFB的面积,即阴影部分的面积.
| 2 |
| 3 |
| 2 |
| 5 |

解答:解:过D作DM‖BF交AC于M(如图)因为BD=2DC,
因为AE=DE,所以△ABE的面积与△DBE的面积相等
所以阴影部分的面积为△DBE的面积+△AEF的面积
DM‖BF所以△DMC相似△CBF 所以CM:CF=CD:CB=1:3
即FM=
CF
因为EF是△ADM的中位线,AF=MF,
所以AF=
AC
所以△ABF的面积10×
=4(平方厘米)
即阴影部分的面积(即△DBE的面积加△AEF的面积)等于4平方厘米
答:阴影部分的面积是4平方厘米,
故答案为:4.
因为AE=DE,所以△ABE的面积与△DBE的面积相等
所以阴影部分的面积为△DBE的面积+△AEF的面积
DM‖BF所以△DMC相似△CBF 所以CM:CF=CD:CB=1:3
即FM=
| 2 |
| 3 |
因为EF是△ADM的中位线,AF=MF,
所以AF=
| 2 |
| 5 |
所以△ABF的面积10×
| 2 |
| 5 |
即阴影部分的面积(即△DBE的面积加△AEF的面积)等于4平方厘米
答:阴影部分的面积是4平方厘米,
故答案为:4.
点评:本题主要是利用在三角形中,高一定,面积与底成正比关系解决问题.

练习册系列答案
相关题目
 如图,p-ABC是一个四面体,各棱互不相等.现用红、黄两种颜色将四面染色,规则如下:
如图,p-ABC是一个四面体,各棱互不相等.现用红、黄两种颜色将四面染色,规则如下: 如图,我们称三个顶点都在正方体的同一个面上的三角形为“面三角形”,如△ABC是“面三角形”,而△ABC1不是“面三角形”,称三个顶点都是红点的“面三角形”为红色“面三角形”.那么最少要将正方体的
如图,我们称三个顶点都在正方体的同一个面上的三角形为“面三角形”,如△ABC是“面三角形”,而△ABC1不是“面三角形”,称三个顶点都是红点的“面三角形”为红色“面三角形”.那么最少要将正方体的