题目内容
(1)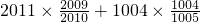
(2)( x-9)×
x-9)× =x-9
=x-9
(3)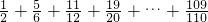
(4)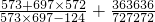
(5)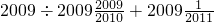
(6)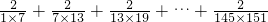 .
.
解:(1)2011× +1004×
+1004× ,
,
=(2010+1)× +(1005-1)×
+(1005-1)× ,
,
=2010× +
+ +1005×
+1005× -
- ,
,
=2009+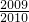 +1004-
+1004-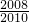 ,
,
=3013+ ,
,
=3013 ;
;
(2)( x-9)×
x-9)× =x-9,
=x-9,
( x-9)×
x-9)× ×5=(x-9)×5,
×5=(x-9)×5,
 x-9=5x-45,
x-9=5x-45,
 x-9+9=5x-45+9,
x-9+9=5x-45+9,
 x=5x-36,
x=5x-36,
 x-
x- x=5x-36-
x=5x-36- x,
x,
4 x-36=0,
x-36=0,
4 x-36+36=0+36,
x-36+36=0+36,
 x=36,
x=36,
 x×
x× =36×
=36× ,
,
x=8;
(3)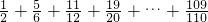 ,
,
=1- +1-
+1- +1-
+1- +1-
+1- +…+1-
+…+1- ,
,
=1+1+…+1-( +
+ +
+ +
+ +…+
+…+ ),
),
=10-(1- +
+ -
- +
+ -
- +…+
+…+ -
- ),
),
=10-(1- ),
),
=10-1+ ,
,
=9 ;
;
(4)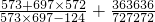 ,
,
= +
+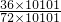 ,
,
= +
+ ,
,
=1+ ,
,
=1 ;
;
(5)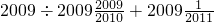 ,
,
=2009÷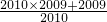 +2009+
+2009+ ,
,
=2009× +2009+
+2009+ ,
,
= +
+ +2009,
+2009,
=1+2009,
=2010;
(6)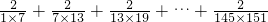 ,
,
= ×(
×(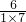 +
+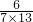 +
+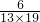 +…+
+…+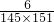 )
)
= ×(1-
×(1- +
+ -
- +
+ -
-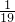 +…
+…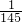 -
- )
)
= ×(1-
×(1- )
)
= ×
× ,
,
=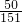 .
.
分析:(1)把2011看作2010+1,把1004看作1005-1,把加号左右两边的每个算式运用乘法分配律简算;
(2)根据等式的性质,两边同乘5,得 x-9=5x-45,两边同加9,得
x-9=5x-45,两边同加9,得 x=5x-36,两边同减去
x=5x-36,两边同减去 x,得4
x,得4 x-36=0,两边同加36,再同乘
x-36=0,两边同加36,再同乘 即可;
即可;
(3)通过观察,每个分数的分子都比分母小1,于是把原式变为1- +1-
+1- +1-
+1- +1-
+1- +…+1-
+…+1- ,把1加在一起,分数加在一起,每个分数可以拆成两个分数相减的形式,然后通过加减相抵消的方法,求得结果;
,把1加在一起,分数加在一起,每个分数可以拆成两个分数相减的形式,然后通过加减相抵消的方法,求得结果;
(4)第一个分数的分子经变化,与分母相同,结果为1;把第二个分数的分子与分母通过变形,化为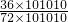 =
= ;
;
(5)加号前的算式,把除数化为假分数时,分子不必算出来,可以通过约分进行计算;2009 写成2009+
写成2009+ ,
,
结算得出;
(6)通过观察,每个分数的分子都为2,分母中的两个因数大6,所以把2× =
= 提出来,原式变为
提出来,原式变为 ×(
×(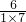 +
+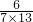 +
+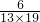 +…+
+…+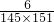 ),然后把括号内的每个分数拆成两个分数相减的形式,通过分数加减相互抵消,得出结果.
),然后把括号内的每个分数拆成两个分数相减的形式,通过分数加减相互抵消,得出结果.
点评:对于这种巧算的题目,应仔细审题,运用所学知识,以及数与数之间的联系,抓住特点,巧妙解答.
 +1004×
+1004× ,
,=(2010+1)×
 +(1005-1)×
+(1005-1)× ,
,=2010×
 +
+ +1005×
+1005× -
- ,
,=2009+
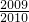 +1004-
+1004-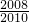 ,
,=3013+
 ,
,=3013
 ;
;(2)(
 x-9)×
x-9)× =x-9,
=x-9,(
 x-9)×
x-9)× ×5=(x-9)×5,
×5=(x-9)×5, x-9=5x-45,
x-9=5x-45, x-9+9=5x-45+9,
x-9+9=5x-45+9, x=5x-36,
x=5x-36, x-
x- x=5x-36-
x=5x-36- x,
x,4
 x-36=0,
x-36=0,4
 x-36+36=0+36,
x-36+36=0+36, x=36,
x=36, x×
x× =36×
=36× ,
,x=8;
(3)
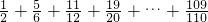 ,
,=1-
 +1-
+1- +1-
+1- +1-
+1- +…+1-
+…+1- ,
,=1+1+…+1-(
 +
+ +
+ +
+ +…+
+…+ ),
),=10-(1-
 +
+ -
- +
+ -
- +…+
+…+ -
- ),
),=10-(1-
 ),
),=10-1+
 ,
,=9
 ;
;(4)
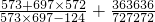 ,
,=
 +
+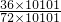 ,
,=
 +
+ ,
,=1+
 ,
,=1
 ;
;(5)
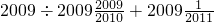 ,
,=2009÷
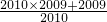 +2009+
+2009+ ,
,=2009×
 +2009+
+2009+ ,
,=
 +
+ +2009,
+2009,=1+2009,
=2010;
(6)
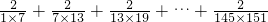 ,
,=
 ×(
×(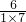 +
+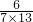 +
+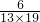 +…+
+…+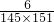 )
)=
 ×(1-
×(1- +
+ -
- +
+ -
-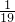 +…
+…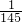 -
- )
)=
 ×(1-
×(1- )
)=
 ×
× ,
,=
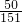 .
.分析:(1)把2011看作2010+1,把1004看作1005-1,把加号左右两边的每个算式运用乘法分配律简算;
(2)根据等式的性质,两边同乘5,得
 x-9=5x-45,两边同加9,得
x-9=5x-45,两边同加9,得 x=5x-36,两边同减去
x=5x-36,两边同减去 x,得4
x,得4 x-36=0,两边同加36,再同乘
x-36=0,两边同加36,再同乘 即可;
即可;(3)通过观察,每个分数的分子都比分母小1,于是把原式变为1-
 +1-
+1- +1-
+1- +1-
+1- +…+1-
+…+1- ,把1加在一起,分数加在一起,每个分数可以拆成两个分数相减的形式,然后通过加减相抵消的方法,求得结果;
,把1加在一起,分数加在一起,每个分数可以拆成两个分数相减的形式,然后通过加减相抵消的方法,求得结果;(4)第一个分数的分子经变化,与分母相同,结果为1;把第二个分数的分子与分母通过变形,化为
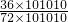 =
= ;
;(5)加号前的算式,把除数化为假分数时,分子不必算出来,可以通过约分进行计算;2009
 写成2009+
写成2009+ ,
,结算得出;
(6)通过观察,每个分数的分子都为2,分母中的两个因数大6,所以把2×
 =
= 提出来,原式变为
提出来,原式变为 ×(
×(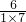 +
+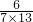 +
+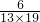 +…+
+…+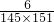 ),然后把括号内的每个分数拆成两个分数相减的形式,通过分数加减相互抵消,得出结果.
),然后把括号内的每个分数拆成两个分数相减的形式,通过分数加减相互抵消,得出结果.点评:对于这种巧算的题目,应仔细审题,运用所学知识,以及数与数之间的联系,抓住特点,巧妙解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 x﹣9)×
x﹣9)× =x﹣9
=x﹣9


