题目内容
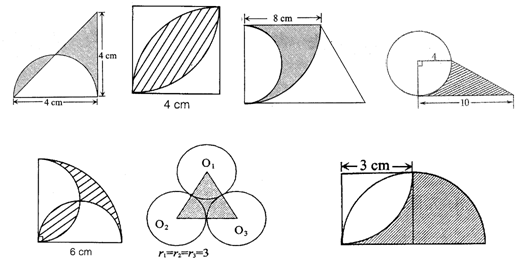
分析:(1)观察图可知,左边的阴影部分可以割补到右边阴影部分的下面,据此可知阴影部分的面积等于图中底和高都是4cm的等腰直角三角形面积的一半;
(2)用扇形面积的2倍减去正方形的面积就是阴影部分的面积,其中扇形的半径为4cm、圆心角为90度,因此面积等于半径为4cm的圆面积的
;正方体的边长为4cm,利用圆面积及正方形的面积公式解决即可;
(3)阴影部分的面积等于半径为8cm的
圆的面积减去直径为8cm的
圆的面积;
(4)阴影部分的面积等于上下底分别为4、10,高为4的梯形的面积减去半径为4的
圆的面积;
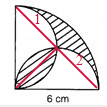
(5)如下图所示,下面阴影部分可以割补到空白部分1和2,可见,阴影部分的面积等于半径为6cm的
圆的面积减去直角边为6cm的等腰直角三角形的面积;
(6)阴影部分是一个边长为6的等边三角形,因此求阴影部分的面积就是求边长为6的等边三角形O1O2O3的面积.如下图作辅助线:
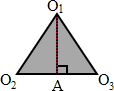
由等边三角形的轴对称性,求得O2A的长,由勾股定理即可求得O1A的长,继而由三角形的面积公式代入数值求得答案;
(7)观察图可知,运用面积割补法,可以把右边阴影部分移到左边正方形中的空白中,由此可见阴影部分的面积就等于正方形的面积.
(2)用扇形面积的2倍减去正方形的面积就是阴影部分的面积,其中扇形的半径为4cm、圆心角为90度,因此面积等于半径为4cm的圆面积的
| 1 |
| 4 |
(3)阴影部分的面积等于半径为8cm的
| 1 |
| 4 |
| 1 |
| 2 |
(4)阴影部分的面积等于上下底分别为4、10,高为4的梯形的面积减去半径为4的
| 1 |
| 4 |
(5)如下图所示,下面阴影部分可以割补到空白部分1和2,可见,阴影部分的面积等于半径为6cm的
| 1 |
| 4 |

(6)阴影部分是一个边长为6的等边三角形,因此求阴影部分的面积就是求边长为6的等边三角形O1O2O3的面积.如下图作辅助线:

由等边三角形的轴对称性,求得O2A的长,由勾股定理即可求得O1A的长,继而由三角形的面积公式代入数值求得答案;
(7)观察图可知,运用面积割补法,可以把右边阴影部分移到左边正方形中的空白中,由此可见阴影部分的面积就等于正方形的面积.
解答:解:(1)4×4÷2÷2=4(cm2);
答:阴影部分的面积是4cm2.
(2)
×3.14×42×2-4×4,
=25.12-16
=9.12(cm2);
答:阴影部分的面积是9.12cm2.
(3)
×3.14×82-
×3.14×(8÷2)2,
=50.24-25.12
=25.12(cm2);
答:阴影部分的面积是25.12cm2.
(4)
×(4+10)×4-
×3.14×42,
=28-12.56
=15.44;
答:阴影部分的面积是15.44.
(5)
×3.14×62-6×6÷2,
=28.26-18
=10.26(cm2);
答:阴影部分的面积是10.26cm2.
(6)由分析可知,O1O2=6,
O2A=
O2O3=
×6=3,
O1A=
=
=3
,
所以三角形O1O2O3的面积是:
×6×3
=9
.
答:阴影部分的面积是9
.
(7)3×3=9(cm2).
答:阴影部分的面积是9cm2.
答:阴影部分的面积是4cm2.
(2)
| 1 |
| 4 |
=25.12-16
=9.12(cm2);
答:阴影部分的面积是9.12cm2.
(3)
| 1 |
| 4 |
| 1 |
| 2 |
=50.24-25.12
=25.12(cm2);
答:阴影部分的面积是25.12cm2.
(4)
| 1 |
| 2 |
| 1 |
| 4 |
=28-12.56
=15.44;
答:阴影部分的面积是15.44.
(5)
| 1 |
| 4 |
=28.26-18
=10.26(cm2);
答:阴影部分的面积是10.26cm2.
(6)由分析可知,O1O2=6,
O2A=
| 1 |
| 2 |
| 1 |
| 2 |
O1A=
| 62-32 |
| 27 |
| 3 |
所以三角形O1O2O3的面积是:
| 1 |
| 2 |
| 3 |
| 3 |
答:阴影部分的面积是9
| 3 |
(7)3×3=9(cm2).
答:阴影部分的面积是9cm2.
点评:求组合图形的面积,比较常用的方法是面积割补法,把阴影部分割补成规则的图形,然后利用公式解决,或者利用规则图形的面积的和差来求组合图形的面积.

练习册系列答案
相关题目
