题目内容
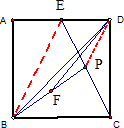
 如图,已知正方形ABCD的边长是4,E、P、F分别是AD、CE、BP的中点,求△DBF的面积.
如图,已知正方形ABCD的边长是4,E、P、F分别是AD、CE、BP的中点,求△DBF的面积.分析:如图所示,连接DP,求出S△BDP,再根据F为BP的中点,可得S△BDP=2S△BDF,问题可解.

解答:解:连接DP,
S△BDP=S△BDC-S△DPC-S△BPC,
=
-
×1×
-
×1×
,
=
,
又因F为BP的中点,
所以P到BD的距离为F到BD的距离的2倍.
S△BDP=2S△BDF,
S△BDF=
,
正方形ABCD的边长为4,
所以S△BDF=
×42=1.
答:△BFD的面积为1.
S△BDP=S△BDC-S△DPC-S△BPC,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
=
| 1 |
| 8 |
又因F为BP的中点,
所以P到BD的距离为F到BD的距离的2倍.
S△BDP=2S△BDF,
S△BDF=
| 1 |
| 16 |
正方形ABCD的边长为4,
所以S△BDF=
| 1 |
| 16 |
答:△BFD的面积为1.
点评:此题主要考查正方形的性质和三角形面的计算,解答此题的关键是作好辅助线,连接DP,根据F为BP的中点,可得S△BDP=2S△BDF.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 一个长方形的纸剪去一个正方形后,剩下如图.
一个长方形的纸剪去一个正方形后,剩下如图.  在正方形ABCD中,如图,已知AB=4厘米,AF=5厘米,则DE的长是多少厘米?
在正方形ABCD中,如图,已知AB=4厘米,AF=5厘米,则DE的长是多少厘米? 如图,已知正方形ABCD的边长为10,若以A为圆心,10为半径,画扇形ABD;在扇形ABD内作⊙O与AD、AB、弧都相切,求⊙O的周长.
如图,已知正方形ABCD的边长为10,若以A为圆心,10为半径,画扇形ABD;在扇形ABD内作⊙O与AD、AB、弧都相切,求⊙O的周长. 在正方形ABCD中,如图,已知AB=4厘米,AF=5厘米,则DE的长是多少厘米?
在正方形ABCD中,如图,已知AB=4厘米,AF=5厘米,则DE的长是多少厘米? 一个长方形的纸剪去一个正方形后,剩下如图.
一个长方形的纸剪去一个正方形后,剩下如图.