Question

五边形ABCDE的每边长均为100米，甲从A出发，依A→B→C→D→…的方向以每分钟70米的速度行走；乙从E出发，依E→A→B→…的方向以每分钟55米的速度行走，则

150

7

分钟后两人第一次走在同一条边上．

Answer 1

分析：由正五边形ABCDE的边长为100米；甲、乙两人分别从A，E两点同时出发时距离是400米，若甲、乙两人第一次行走在同一条边上时，极有可能此时距离为一条边长100米，此时时间为300÷（70-55）=20分．而就在此时，甲、乙分别在点E、A处，不在同一条边上，需继续前行，则甲至少还需走100米，即

10

7

分，此时甲在点F，乙在边FA上，也就是说出发后经过

150

7

分钟，甲乙两人第一次行走在同一条边上．

解答：解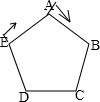：（400-100）÷（70-55）
=300÷15
=20（分）．
100÷70=

10

7

（分），
20+

10

7

=

150

7

（分）．
答：出发后经过

150

7

分钟，甲乙两人第一次行走在同一条边上．
故答案为：

150

7

．

点评：这是一道发散性的题．注意反证思想的应用．此题属于追及问题与正五边形知识的综合应用．