Question

在一个正六边形中，找出一个三角形，使这个三角形的面积等于正六边形面积的

1

3

．（直接在图4中画出，并说明理由）

Answer 1

考点：图形划分

专题：平面图形的认识与计算

分析：经过正六边形的中心O点，连接六个顶点分成六个小正三角形，要使要求的大三角形的面积等于正六边形面积的

1

3

，必须使大三角形的面积等于两个小正三角形的面积和，因为平行四边形ABCO是由两个小正三角形构成的，所以三角形ACO的面积等于一个小正三角形的面积，它与三角形CDO正好构成了一个大三角形ACD，因此三角形ACD的面积就等于正六边形面积的

1

3

，据此画图即可．

解答： 解：根据分析画图如下：

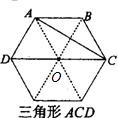
其中三角形的面积ACD就等于正六边形面积的

1

3

．

点评：本题关键是先构建成六个面积相等的小正三角形，然后根据等底等高的三角形面积相等，把两个三角形转化为一个符合要求的大三角形，问题得解．