题目内容
一个等腰三解形一个底角是一个顶角的
，这个等腰三角形的一个底角是
| 1 | 4 |
30
30
度．一个直角三角形的一个锐角和另一个锐角比是4：5，这个三角形中最小角是40
40
度．分析：（1）设这个三角形的底角的度数为x，则可以得到x+x+4x=180°，解此方程即可得解；
（2）因为直角三角形中两个锐角的度数之和为90度，它们的比已知，于是利用按比例分配的方法，即可得解．
（2）因为直角三角形中两个锐角的度数之和为90度，它们的比已知，于是利用按比例分配的方法，即可得解．
解答：解：（1）设这个三角形的底角的度数为x，
x+x+4x=180°，
6x=180°，
x=30°；
（2）90°×
=40°．
故答案为：30、40．
x+x+4x=180°，
6x=180°，
x=30°；
（2）90°×
| 4 |
| 4+5 |
故答案为：30、40．
点评：此题主要依据三角形的内角和定理解决实际问题．
练习册系列答案
小学能力测试卷系列答案
相关题目
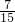，用这两种木条三根围成一个等腰三解形，等腰三角形的周长是_____厘米．