题目内容
 如图,已知边长为8的正方形ABCD,E为AD的中点,P为CE的中点,△BDP的面积
如图,已知边长为8的正方形ABCD,E为AD的中点,P为CE的中点,△BDP的面积8
8
.分析:连接BE,因为E为AD的中点,则△BEC的面积等于正方形ABCD的面积的一半,又因为P为CE的中点,所以△BPC的面积等于△BEC的面积的一半,根据三角形的面积公式求出三角形CDE的面积,而△CDP的面积等于△CDE的面积的一半,
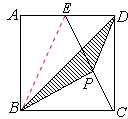

解答:解:连接BE,因为E为AD的中点,
所以△BEC的面积=
×正方形ABCD的面积=
×8×8=32;
因为P为CE的中点,所以△BPC的面积=
×△BEC的面积=16;
△CDE的面积=
×8×4=16;
△CDP的面积=
×△CDE的面积=
×16=8.
而△ABD的面积=
×8×8=32.
所以△BDP的面积=正方形ABCD的面积-△ABD的面积-△BPC的面积-△DPC的面积=64-32-16-8=8.
故答案为:8.
所以△BEC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
因为P为CE的中点,所以△BPC的面积=
| 1 |
| 2 |
△CDE的面积=
| 1 |
| 2 |
△CDP的面积=
| 1 |
| 2 |
| 1 |
| 2 |
而△ABD的面积=
| 1 |
| 2 |
所以△BDP的面积=正方形ABCD的面积-△ABD的面积-△BPC的面积-△DPC的面积=64-32-16-8=8.
故答案为:8.
点评:解答此题的关键是利用三角形的面积公式及高一定时,面积与底成正比的性质解决问题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,边长为8厘米和6厘米的正方形纸片重叠地放在桌子上.已知A、B是大正方形的中点,它们盖住桌面的面积是多少平方厘米?
如图,边长为8厘米和6厘米的正方形纸片重叠地放在桌子上.已知A、B是大正方形的中点,它们盖住桌面的面积是多少平方厘米? 如图已知正方形ABCD和正方形DEFM,且正方形ABCD的边长为8分米.请问图中阴影部分的面积是多少平方分米?
如图已知正方形ABCD和正方形DEFM,且正方形ABCD的边长为8分米.请问图中阴影部分的面积是多少平方分米?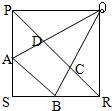 如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是
如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是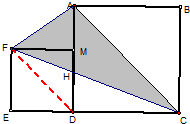 如图已知正方形ABCD和正方形DEFM,且正方形ABCD的边长为8分米.请问图中阴影部分的面积是多少平方分米?
如图已知正方形ABCD和正方形DEFM,且正方形ABCD的边长为8分米.请问图中阴影部分的面积是多少平方分米?