题目内容
列式计算.
(1)把 与
与 的和扩大到原来的3倍,得多少?
的和扩大到原来的3倍,得多少?
(2) 的倒数与
的倒数与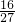 的积是多少?
的积是多少?
(3) 的倒数加上一个数等于最小的质数,这个数是多少?
的倒数加上一个数等于最小的质数,这个数是多少?
解:(1)( +
+ )×3,
)×3,
= ×3,
×3,
= ;
;
答:扩大到原来的3倍,得 .
.
(2)1÷ ×
×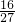 ,
,
= ×
×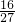 ,
,
= ;
;
答:积是 .
.
(3)2-1÷ ,
,
=2- ,
,
= ;
;
答:这个数是 .
.
分析:(1) 与
与 的和是(
的和是( +
+ ),扩大3倍后就是(
),扩大3倍后就是( +
+ )×3,解决问题;
)×3,解决问题;
(2)求积,根据题意,就是两个数相乘,即 与
与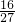 相乘;
相乘;
(3)最小的质数是2, 的倒数是
的倒数是 ,即
,即 加上一个数等于2,在没加这个数之前是2-
加上一个数等于2,在没加这个数之前是2- ,解决问题.
,解决问题.
点评:(1)先求和,再求积;
(2)理解倒数概念,然后求两个数的积;
(3)理解质数与倒数概念,是解答此题的关键.
 +
+ )×3,
)×3,=
 ×3,
×3,=
 ;
;答:扩大到原来的3倍,得
 .
.(2)1÷
 ×
×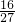 ,
,=
 ×
×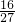 ,
,=
 ;
;答:积是
 .
.(3)2-1÷
 ,
,=2-
 ,
,=
 ;
;答:这个数是
 .
.分析:(1)
 与
与 的和是(
的和是( +
+ ),扩大3倍后就是(
),扩大3倍后就是( +
+ )×3,解决问题;
)×3,解决问题;(2)求积,根据题意,就是两个数相乘,即
 与
与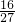 相乘;
相乘;(3)最小的质数是2,
 的倒数是
的倒数是 ,即
,即 加上一个数等于2,在没加这个数之前是2-
加上一个数等于2,在没加这个数之前是2- ,解决问题.
,解决问题.点评:(1)先求和,再求积;
(2)理解倒数概念,然后求两个数的积;
(3)理解质数与倒数概念,是解答此题的关键.

练习册系列答案
相关题目