Question

（2007?延庆县）根据下列概念间的逻辑关系填空．
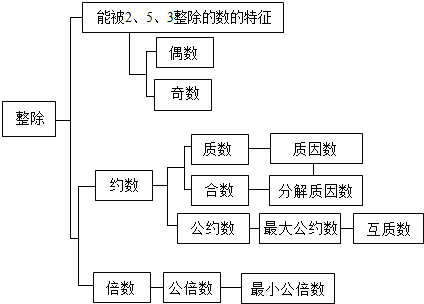
约数      能被2、5、3整除的数的特征    倍数
公约数        质数       公倍数        互质数
合数          质因数     奇数        最大公约数
最小公倍数    偶数       整除        分解质因数．

Answer 1

分析：（1）根据能被2整除的数叫做偶数，不能被2整除的数叫做奇数，可填出最上边的两个方框；
（2）根据整数a除以整数b，如果除得的商正好是整数而没有余数，我们就说a能被b整除，或者说b能整除a，其中a叫做b的倍数，b叫做a的约数，由此可填出倍数上面的方框；
（3）根据一个数含有约数的个数即如果只有1和它本身两个约数叫做质数，如果除了1和它本身，还有别的约数叫做合数，所以质数下面的方框填合数；再根据把一个合数用质因数相乘的形式表示出来，叫做分解质因数，可填出合数右边的方框；
（4）根据几个数共有的约数叫做这几个数的公约数，其中最大的一个叫做最大公约数可得出，公约数右边的方框；
（5）根据几个数共有的倍数叫做这几个数的公倍数，其中最小的一个叫做最小公倍数可得出，最后一行的两个方框．

解答：解：

点评：此题考查了有关整除知识的逻辑关系．