题目内容
 在三角形ABC中,点E是BC边上的中点,点F是中线AE上的点,其中AE=3AF,并且延长BF与AC相交于D,如下图所示.若三角形ABC的面积为48,请问三角形AFD的面积是
在三角形ABC中,点E是BC边上的中点,点F是中线AE上的点,其中AE=3AF,并且延长BF与AC相交于D,如下图所示.若三角形ABC的面积为48,请问三角形AFD的面积是1.6
1.6
.分析:连接DE,如图根据在三角形中,高一定,底与面积成正比的关系,分别求出三角形AEB与三角形AEC的面积,进而求出三角形ABF与三角形BEF的面积,由此设三角形AFD的面积是S,则
三角形ADF的面积+三角形DEF的面积+三角形DEC的面积=三角形AEC的面积,即可求出三角形AFD的面积.

三角形ADF的面积+三角形DEF的面积+三角形DEC的面积=三角形AEC的面积,即可求出三角形AFD的面积.

解答:解:因为点F是中线AE上的点,
所以S△ABE=S△AEC=48÷2=24,
因为AE=3AF,
所以S△ABF:S△ABE=1:3,
所以S△ABF=
×24=8,
S△BEF=24-8=16,
而S△BDE=S△DEC,
S△DFE=2S△ADF,
所以设三角形AFD的面积是S;
三角形ADF的面积+三角形DEF的面积+三角形DEC的面积=三角形AEC的面积,
则S+2S+2S+16=24,
5S=8,
S=1.6;
答:三角形AFD的面积是1.6.
所以S△ABE=S△AEC=48÷2=24,
因为AE=3AF,
所以S△ABF:S△ABE=1:3,
所以S△ABF=
| 1 |
| 3 |
S△BEF=24-8=16,
而S△BDE=S△DEC,
S△DFE=2S△ADF,
所以设三角形AFD的面积是S;
三角形ADF的面积+三角形DEF的面积+三角形DEC的面积=三角形AEC的面积,
则S+2S+2S+16=24,
5S=8,
S=1.6;
答:三角形AFD的面积是1.6.
点评:此题主要考查了高一定,底与面积成正比的关系的灵活应用.

练习册系列答案
相关题目
 在三角形ABC中,D是BC的一个三等分点,E是AC的中点,AD和BE把三角形分成四块,其面积分别为S1、S2、S3、S4(如图所思)已知S1比S2大7平方厘米,S3的面积为18平方厘米;求△ABC的面积.
在三角形ABC中,D是BC的一个三等分点,E是AC的中点,AD和BE把三角形分成四块,其面积分别为S1、S2、S3、S4(如图所思)已知S1比S2大7平方厘米,S3的面积为18平方厘米;求△ABC的面积.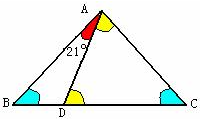 如图,在三角形ABC中,点D在BC上,且∠ABC=∠ACB、∠ADC=∠DAC,∠DAB=21°,求∠ABC的度数;并回答:图中哪些三角形是锐角三角形.
如图,在三角形ABC中,点D在BC上,且∠ABC=∠ACB、∠ADC=∠DAC,∠DAB=21°,求∠ABC的度数;并回答:图中哪些三角形是锐角三角形. 如图,在三角形ABC中,AE=ED,D点是BC的四等分点,阴影部分的面积占三角形ABC面积的几分之几?
如图,在三角形ABC中,AE=ED,D点是BC的四等分点,阴影部分的面积占三角形ABC面积的几分之几?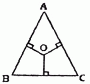 如图,在三角形ABC中有一点O,O点到三条边的垂线长都是2厘米,又知道三角形的周长是20厘米,那么三角形ABC的面积是
如图,在三角形ABC中有一点O,O点到三条边的垂线长都是2厘米,又知道三角形的周长是20厘米,那么三角形ABC的面积是