题目内容
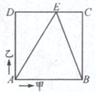 如图,甲、乙两人按箭头方向从A点同时出发,沿亠正方形ABCD的边行走,正方形ABCD的边长是100米,甲的速度是乙的速度的1.5倍,两人在E点第一次相遇,则三角形ADE的面积比三角形BCE的面积大
如图,甲、乙两人按箭头方向从A点同时出发,沿亠正方形ABCD的边行走,正方形ABCD的边长是100米,甲的速度是乙的速度的1.5倍,两人在E点第一次相遇,则三角形ADE的面积比三角形BCE的面积大1000
1000
平方米.分析:这是一道行程与几何结合起来的综合题.要想知道三角形ADE的面积比三角形BCE的面积大多少平方米,就要明确DE及EC的长度是多少,由于相遇问题中,速度比=所行路程的比,因此通过周长及两人的速度比可求出两人相遇时各行的路程是多少,进行求出DE及EC的长度之后,再据三角形的面积公式就能求出三角形ADE的面积比三角形BCE的面积大多少平方米了.
解答:解: 由于甲的速度是乙的速度的1.5倍所以两人速度比为:1.5:1=3:2,
由于甲的速度是乙的速度的1.5倍所以两人速度比为:1.5:1=3:2,
所以两人在E点相遇时,甲行了:(100×4)×
=240(米);
乙行了:400-240=160(米);
则EC=240-100×2=40(米),DE=160-100=60(米);
三角形ADE的面积比三角形BCE的面积大:
60×100÷2-40×100÷2
=3000-2000,
=1000(平方米).
故答案为:1000.
 由于甲的速度是乙的速度的1.5倍所以两人速度比为:1.5:1=3:2,
由于甲的速度是乙的速度的1.5倍所以两人速度比为:1.5:1=3:2,所以两人在E点相遇时,甲行了:(100×4)×
| 3 |
| 3+2 |
乙行了:400-240=160(米);
则EC=240-100×2=40(米),DE=160-100=60(米);
三角形ADE的面积比三角形BCE的面积大:
60×100÷2-40×100÷2
=3000-2000,
=1000(平方米).
故答案为:1000.
点评:根据两人的速度比求出两人相遇时各行了多少千米进而求出DE、EC的长度是完成本题的关健.

练习册系列答案
相关题目
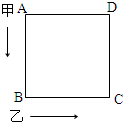 如图,甲、乙两人沿着边长为90米的正方形,按A→B→C→D→A…方向,甲从A以65米/分的速度,乙从B以72米/分的速度同时行走,当乙第一次追上甲时在正方形的( )
如图,甲、乙两人沿着边长为90米的正方形,按A→B→C→D→A…方向,甲从A以65米/分的速度,乙从B以72米/分的速度同时行走,当乙第一次追上甲时在正方形的( )| A、AB边上 | B、DA边上 | C、BC边上 | D、CD边上 |
 】
】 如图,甲、乙两人分别从圆形跑道直径AB两端同时出发相向而行.在离A点90米处的C地相遇,两人继续前进,再一次相遇时是在离B点113米的D处,这个圆形的面积是
如图,甲、乙两人分别从圆形跑道直径AB两端同时出发相向而行.在离A点90米处的C地相遇,两人继续前进,再一次相遇时是在离B点113米的D处,这个圆形的面积是 如图,甲、乙两人按箭头方向从A点同时出发,沿亠正方形ABCD的边行走,正方形ABCD的边长是100米,甲的速度是乙的速度的1.5倍,两人在E点第一次相遇,则三角形ADE的面积比三角形BCE的面积大________平方米.
如图,甲、乙两人按箭头方向从A点同时出发,沿亠正方形ABCD的边行走,正方形ABCD的边长是100米,甲的速度是乙的速度的1.5倍,两人在E点第一次相遇,则三角形ADE的面积比三角形BCE的面积大________平方米.