题目内容
正方形ABCD边长是4cm,又知AE=5cm,那么DF=
3.2
3.2
cm.
分析:连结DE,由于由于三角形ABE的面积+三角形ECD的面积=
BE×AB+
EC×AB=
AB(BE+EC)=
AB×BC=
×4×4=8(cm2),由此得出三角形DAE的面积=正方形ABCD的面积-8=4×4-8=8(cm2),在三角形DAE中,由于DF是底AE上的高,即可求出DF.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:如图,连结DE,

由于三角形ABE和三角形ECD的两底和是正方形的边长,高也是正方形的边长,
所以三角形ABE的面积+三角形ECD的面积
=(BE+EC)×AB÷2
=4×4÷2
=8(cm2),
所以三角形DAE的面积
=4×4-8
=8(cm2)
DF=8×2÷5
=3.2(cm);
故答案为:3.2

由于三角形ABE和三角形ECD的两底和是正方形的边长,高也是正方形的边长,
所以三角形ABE的面积+三角形ECD的面积
=(BE+EC)×AB÷2
=4×4÷2
=8(cm2),
所以三角形DAE的面积
=4×4-8
=8(cm2)
DF=8×2÷5
=3.2(cm);
故答案为:3.2
点评:解答此题的关键连连DE,由于三角形ABE的面积+三角形ECD的面积是正方形面积的一半,因此三角形DAE的面积也是正方形面积的一半,进而求出三角形DAE的高DF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图:正方形ABCD边长是6厘米,三角形(甲)AFD是正方形的一部分,三角形(乙)FCE的面积比甲三角形大6平方厘米,求CE长多少厘米?
如图:正方形ABCD边长是6厘米,三角形(甲)AFD是正方形的一部分,三角形(乙)FCE的面积比甲三角形大6平方厘米,求CE长多少厘米?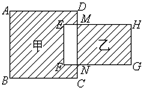 如图正方形ABCD边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.阴影部分甲与阴影部分乙的面积差是
如图正方形ABCD边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.阴影部分甲与阴影部分乙的面积差是
