题目内容
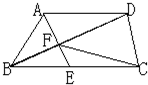 梯形ABCD中,AE与DC平行,S△ABE=15,S△BCF=
梯形ABCD中,AE与DC平行,S△ABE=15,S△BCF=15
15
.分析:连接DE,因为AE与DC平行,根据等底(EF)同高的两个三角形的面积相等,得出S△DEF=S△CEF,再根据等底(AD)同高的两个三角形的面积相等,得出 S△ABD=S△AED,所以,S△ABD-S△AFD=S△AED-S△AFD,即S△ABF=S△DEF,所以S△ABF=S△CEF,由此即可得出答案.
解答:解:连接DE,
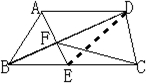
因为AE与DC平行,
根据等底(EF)同高的两个三角形的面积相等,得出S△DEF=S△CEF,
再根据等底(AD)同高的两个三角形的面积相等,得出 S△ABD=S△AED,
所以,S△ABD-S△AFD=S△AED-S△AFD,即S△ABF=S△DEF,
所以S△ABF=S△CEF,那么S△ABF+SBEF=S△CEF+SBEF,
即S△ABE=S△BCF=15,
故答案为:15.

因为AE与DC平行,
根据等底(EF)同高的两个三角形的面积相等,得出S△DEF=S△CEF,
再根据等底(AD)同高的两个三角形的面积相等,得出 S△ABD=S△AED,
所以,S△ABD-S△AFD=S△AED-S△AFD,即S△ABF=S△DEF,
所以S△ABF=S△CEF,那么S△ABF+SBEF=S△CEF+SBEF,
即S△ABE=S△BCF=15,
故答案为:15.
点评:此题主要考查了蝴蝶定理的应用(即在梯形里,等底同高的两个三角形的面积相等).

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
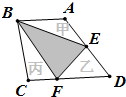 (2013?龙海市模拟)如图,梯形ABCD的面积是35平方厘米,AE=ED,图中三角形甲、乙、丙的面积相等,求阴影部分的面积.
(2013?龙海市模拟)如图,梯形ABCD的面积是35平方厘米,AE=ED,图中三角形甲、乙、丙的面积相等,求阴影部分的面积.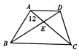 在梯形ABCD中S△ABE=12平方厘米,AE=
在梯形ABCD中S△ABE=12平方厘米,AE=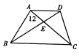 在梯形ABCD中S△ABE=12平方厘米,AE=
在梯形ABCD中S△ABE=12平方厘米,AE= EC,则梯形的面积SABCD=________平方厘米.
EC,则梯形的面积SABCD=________平方厘米.