题目内容
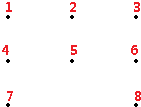
如图是一个3×3的正方形钉阵，其中拔掉了1个钉子．用皮筋去套剩下的8个钉子，共能套出多少个三角形？分析：观察图形可知，把这8个点分别标上序号1、2、3、4、5、6、7、8；从8个点中选出1和另外2个点有：123、124、125、126、127、128、134、135、136、137、138、145、146、147、148、156、157、158、167、168、178，21种选法，其中123、147、158在一条直线上，不能组成三角形，所以与1点连接能组成的三角形有18个；
再从剩下的7个点中选出2和另外2个点有234、235、236、237、238、245、246、247、248、256、257、258、267、268、278一共有15种情况，都能组成三角形；
再从剩下的6个点中选出3和另外2个点有：345、346、347、348、356、357、358、367、368、378，10种选法，其中357、368在一条直线上，不能组成三角形，所以一共有8个三角形；
再从剩下的5个点中选出4和另外2个点有：456、457、458、467、468、478，一共有6种情况，其中456在一条直线上，不能组成三角形，所以能组成5个三角形；
再从剩下的4个点中选出5和另外两个点有：567、568、578，3种选法，都能组成三角形；
最后剩下三个点678，不在一条直线上，能组成三角形；据此把这几种情况下能组成的三角形个数加起来即可解答．
再从剩下的7个点中选出2和另外2个点有234、235、236、237、238、245、246、247、248、256、257、258、267、268、278一共有15种情况，都能组成三角形；
再从剩下的6个点中选出3和另外2个点有：345、346、347、348、356、357、358、367、368、378，10种选法，其中357、368在一条直线上，不能组成三角形，所以一共有8个三角形；
再从剩下的5个点中选出4和另外2个点有：456、457、458、467、468、478，一共有6种情况，其中456在一条直线上，不能组成三角形，所以能组成5个三角形；
再从剩下的4个点中选出5和另外两个点有：567、568、578，3种选法，都能组成三角形；
最后剩下三个点678，不在一条直线上，能组成三角形；据此把这几种情况下能组成的三角形个数加起来即可解答．
解答：解：根据题干分析可得：18+15+8+5+3+1=50个；
答：能连成50个三角形．
答：能连成50个三角形．
点评：此题主要考查三角形的特征和图形计数的方法，不在同一条直线上的三个点都能组成三角形，要注意做到不重不漏，据此即可解答．
练习册系列答案
相关题目
如图是一个公园的平面图，用对数表示各场所在平面图上的位置．
如图是一个101×101的点阵，各点的位置用其下面与左边正对的两数来表示：若某点M下面正对的数是x，左边正对的数是y，则称M的位置为（x，y），如P的位置为（7，3），Q的位置为（4，7）．现有一个粒子从（0，0）出发，沿图示路线运动，且每秒钟移动一个单位长度，即1秒钟后到（1，0），2秒钟后到（1，1），…．
如图，一个正方体木块，它的六个面上分别写着数字1，2，3，4，5，6，其中写着数字1和6的两个面相对，写着数字2和5的两个面相对，写着数字3和4的两面相对．若按图中箭头指示的方向翻动木块，则当木块翻动到C格时，木块正上方那一面的数字是
如图是某单位一个水龙头滴水量随时间变化的关系图，请根据关系图解决下列问题．
如图是一个公园的平面图，用对数表示各场所在平面图上的位置．