题目内容
在一个边长为1的正三角形内,任给5个点,证明:其中必有两个点之间的距离不大于
.
| 1 | 2 |
分析:把小正三角形的个数看作“抽屉”,把5个点看作“物体的个数”,因为物体的个数比抽屉数多一,所以必定有两个点在同一个小正三角形内,进而得出结论.
解答:解:如图,将三角形三边中点连接起来,就将原三角形分成了四个小三角形,其边长均为
,在原三角形内,任意给5个点,其中至少有两点在同一个小三角形内,这两点的距离小于小三角形的边长
.

| 1 |
| 2 |
| 1 |
| 2 |

点评:此类题解答的关键是从最极端情况分析,假设其中的四点分别在4个小三角形内,则第五个点一定在这4个小三角形中,根据抽屉原理进行解答即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013?北京模拟)在桌面上,用6个边长为1的正三角形可以拼成一个边长为1的正六边形(如图).如果在桌面上,要拼一个边长为6的正六边形,那么,需要边长为1的正三角形
(2013?北京模拟)在桌面上,用6个边长为1的正三角形可以拼成一个边长为1的正六边形(如图).如果在桌面上,要拼一个边长为6的正六边形,那么,需要边长为1的正三角形 如图,有一个边长为1的正三角形,第一次去掉三边中点连线围成的那个正三角形;第二次对留下的三个正三角形,再分别去掉它们中点连线围成的三角形;…做到第四次后,一共去掉了
如图,有一个边长为1的正三角形,第一次去掉三边中点连线围成的那个正三角形;第二次对留下的三个正三角形,再分别去掉它们中点连线围成的三角形;…做到第四次后,一共去掉了 如图所示,在一个边长为1的大正方形中有两个小正方形,他们的面积分别为m、n.猜猜看,是m大还是n大?并求
如图所示,在一个边长为1的大正方形中有两个小正方形,他们的面积分别为m、n.猜猜看,是m大还是n大?并求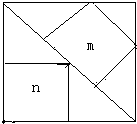 如图所示,在一个边长为1的大正方形中有两个小正方形,他们的面积分别为m、n.猜猜看,是m大还是n大?并求
如图所示,在一个边长为1的大正方形中有两个小正方形,他们的面积分别为m、n.猜猜看,是m大还是n大?并求 的值?
的值?