题目内容
一个圆柱和一个圆锥的底面半径相等，体积相等，则圆柱和圆锥高的比是________．
1：3
分析：一个圆柱和一个圆锥底面半径相等，根据圆的面积公式可知，它们的底面积就相等，由此设圆柱和圆锥的底面积相等是S，体积相等是V，即可求出它们的高的比．
解答：底面半径相等，则这个圆柱与圆锥的底面积就相等，
设圆柱和圆锥的底面积相等是S，体积相等是V，所以它们的高的比是：
：
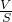=1：3，
答：这个圆柱与圆锥的高的比是1：3．
故答案为：1：3．
点评：此类问题一般是利用圆柱与圆锥的体积公式，即可求出圆柱与圆锥的高的比．
分析：一个圆柱和一个圆锥底面半径相等，根据圆的面积公式可知，它们的底面积就相等，由此设圆柱和圆锥的底面积相等是S，体积相等是V，即可求出它们的高的比．
解答：底面半径相等，则这个圆柱与圆锥的底面积就相等，
设圆柱和圆锥的底面积相等是S，体积相等是V，所以它们的高的比是：
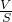：=1：3，答：这个圆柱与圆锥的高的比是1：3．
故答案为：1：3．
点评：此类问题一般是利用圆柱与圆锥的体积公式，即可求出圆柱与圆锥的高的比．
练习册系列答案
相关题目