题目内容
如图,直角三角形纸片ABC中,AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交与点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;…;设Pn-1Dn-2的中点为Dn-1,第n次将纸片折叠,使点A与点Dn-1重合,折痕与AD交于点Pn(n>2),则AP6的长为( )


分析:先写出AD、AD1、AD2、AD3的长度,然后可发现规律推出ADn的表达式,继而根据Apn=
ADn,即可得出APn的表达式,也可得出AP6的长.
| 2 |
| 3 |
解答:解:由题意得,AD=
BC=
,AD1=AD-DD1=
,AD2=
,AD3=
,…,ADn=
,
又因为APn=
ADn,
所以AP1=
,AP2=
,AP3=
…APn=
,
故可得AP6=
.
故选:A.
| 1 |
| 2 |
| 5 |
| 2 |
| 5×31 |
| 23 |
| 5× |
| 5×32 |
| 25 |
| 5×33 |
| 27 |
| 5×3n |
| 22n+1 |
又因为APn=
| 2 |
| 3 |
所以AP1=
| 5 |
| 4 |
| 15 |
| 16 |
| 5×32 |
| 26 |
| 5×3n-1 |
| 22n |
故可得AP6=
| 5×35 |
| 212 |
故选:A.
点评:此题考查了翻折变换的知识,解答本题关键是写出前面几个有关线段长度的表达式,从而得出一般规律,注意培养自己的归纳总结能力.

练习册系列答案
相关题目
 有一张等腰直角三角形的纸片,沿它的斜边上的高把这个三角形对折;再沿斜边上的高把它对折,这时,得到一个直角边的边长是2厘米的等腰直角三角形(如图中的阴影部分),那么,原来的等腰直角三角形纸片的面积是
有一张等腰直角三角形的纸片,沿它的斜边上的高把这个三角形对折;再沿斜边上的高把它对折,这时,得到一个直角边的边长是2厘米的等腰直角三角形(如图中的阴影部分),那么,原来的等腰直角三角形纸片的面积是 用一张斜边长为29的红色直角三角形纸片,一张斜边长为49的蓝色直角三角形纸片,一张黄色的正方形纸片,如图恰拼成一个直角三角形(如图).问:红、蓝两张三角形纸片面积之和是多少?试说明理由.
用一张斜边长为29的红色直角三角形纸片,一张斜边长为49的蓝色直角三角形纸片,一张黄色的正方形纸片,如图恰拼成一个直角三角形(如图).问:红、蓝两张三角形纸片面积之和是多少?试说明理由. 如图,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有
如图,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有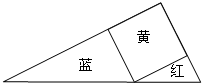 用一张斜边30厘米的红色直角三角形纸片,一张斜边为50厘米的蓝色直角三角形,一张边长为25厘米的黄色的正方形纸片,拼成如图的一个直角三角形.红、蓝两张三角形纸片面积之和是多少平方厘米?
用一张斜边30厘米的红色直角三角形纸片,一张斜边为50厘米的蓝色直角三角形,一张边长为25厘米的黄色的正方形纸片,拼成如图的一个直角三角形.红、蓝两张三角形纸片面积之和是多少平方厘米?