题目内容
 正方形ABCD边长为6厘米,AE=
正方形ABCD边长为6厘米,AE=| 1 |
| 3 |
| 1 |
| 3 |
分析:连接BE,则正方形的空白处的面积就分成了4部分,如图所示;阴影部分的面积=正方形的面积-四个空白处的面积,由此分别求出空白处1、2、3、4的面积即可解决问题.


解答:解:因为AE=
AC,可得空白处1的面积与三角形ABC的面积之比是1:3,
因为三角形ABC的面积是6×6÷2=18(平方厘米),
所以空白处1的面积是18÷3=6(平方厘米),
同理可得空白处4的面积也是6平方厘米;
又因为CF=
BC,所以空白处2的面积与三角形BEC的面积之比是2:3,
三角形BEC的面积就是18-6=12(平方厘米),
所以空白处2的面积是12×
=8(平方厘米);.
空白处3的面积是:6÷3×6÷2=6(平方厘米),
所以阴影部分的面积是:6×6-6-6-8-6,
=36-26,
=10(平方厘米),
答:阴影部分的面积是10平方厘米.
| 1 |
| 3 |
因为三角形ABC的面积是6×6÷2=18(平方厘米),
所以空白处1的面积是18÷3=6(平方厘米),
同理可得空白处4的面积也是6平方厘米;
又因为CF=
| 1 |
| 3 |
三角形BEC的面积就是18-6=12(平方厘米),
所以空白处2的面积是12×
| 2 |
| 3 |
空白处3的面积是:6÷3×6÷2=6(平方厘米),
所以阴影部分的面积是:6×6-6-6-8-6,
=36-26,
=10(平方厘米),
答:阴影部分的面积是10平方厘米.
点评:此题考查了高一定时,三角形的面积与底成正比例的灵活应用.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 如图,正方形ABCD边长为4,K是AB边的中点,L点在它的对角线AC上.且AL是LC的3倍.那么,△KDL的面积是
如图,正方形ABCD边长为4,K是AB边的中点,L点在它的对角线AC上.且AL是LC的3倍.那么,△KDL的面积是
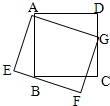 如图,正方形ABCD边长为6分米,长方形AEFG的长AG为7分米,右点G在DC上,点B在EF上,则长方形宽AE是
如图,正方形ABCD边长为6分米,长方形AEFG的长AG为7分米,右点G在DC上,点B在EF上,则长方形宽AE是 ,求CE=?
,求CE=?