Question

将l～9这9个数字填入图34中，使每条边上的四个圆圈内的数之和相等．给出两种不同填法．

Answer 1

分析：设每边四个数之和是S，计算三条边上的和时有3个数被计算了两次，设这三个数的和是d，则（1+2+3+…+9）+d=3S，即45+d=4S，由此，可知d是3的倍数，则其取值范围是：6、9、12、15、18、21、24，其中6=1+2+3，24=7+8+9，因此，据此解答．

解答：解：设每边四个数之和是S，计算三条边上的和时有3个数被计算了两次，
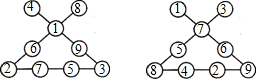
设这三个数的和是d，则（1+2+3+…+9）+d=3S，即45+d=3S，由此，可知d是3的倍数，
则其取值范围是：6、9、12、15、18、21、24，其中：9、12、15、18、21经过验证不符合要求，
只有其中的6=1+2+3，24=7+8+9，符合要求，
因此，对应这两种情况的填法如下图：

点评：本题关键是根据幻和，确定3个被计算了两次的和的取值范围．