Question

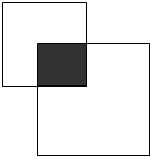如图，两下正方形重叠部分的面积相当于大正方形面积的

1

9

，相当于小正方形面积的

1

4

．大正方形与小正方形面积的比是

9：4

．

Answer 1

分析：根据题意可知，重叠部分的面积既等于大正方形面积的

1

9

，又等于小正方形面积的

1

4

；由此根据分数乘法的意义可以得到一个数量关系式是：大正方形面积×

1

9

=小正方形面积×

1

4

，然后再根据比例的基本性质即两内项之积等于两外项之积，得到一个比例式，进而解比例就可求出大正方形与小正方形面积的比．

解答：解：根据题意可知：
因为大正方形面积×

1

9

=重叠部分的面积=小正方形面积×

1

4

，
所以大正方形面积×

1

9

=小正方形面积×

1

4

，
可得：大正方形面积：小正方形面积=

1

4

：

1

9

=9：4；
答：大正方形与小正方形面积的比是9：4．
故答案为：9：4．

点评：本题考查了比例知识的灵活应用，本题的关键是根据题意找出大正方形面积×

1

9

=小正方形面积×

1

4

，然后列出比例式．