题目内容
【题目】如图，已知直线
和
、
分别交于
、
两点，点
在直线上运动．
（1）若点在
两点之间运动，试探究：当
、
和
之间满足什么数量关系时，
？
（2）若点在两点外侧运动，试探究：当、和之间满足什么数量关系时，？（写出结论，并说明理由）
【答案】（1）
时，
（2）①当点
在点
的下方时，
时，
②当点在点
的上方时，
时，
【解析】
（1）过点作直线
的平行线，要想，两直线平行，那么过点的直线必须和直线
也平行，两直线平行，内错角相等可知；
（2）分两种情况，点在点上方，点在点下方，证明方法同第一问
（1）如图：
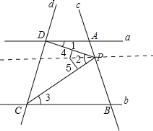
时，
过点作直线的平行线，把
分成
和
所以：
又因为：
所以：
所以：
过点平行的直线也平行于直线
所以：
（2）①当点在点的下方时，如图：
时，
过点作直线的平行线
所以：
因为：
所以：
所以：
所以：
如图：
②当点在点的上方时，如图：
时，
证明方法同上．
所以：时，．
练习册系列答案
相关题目
【题目】根据平均气温统计图完成下面的统计表，并回答问题
2014年北京市、桂林市各季度平均气温统计图
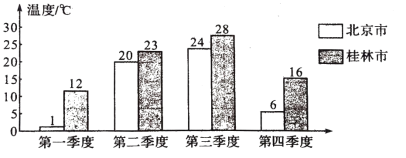
(1)根据统计图完成下表。（年平均气温保留整数）
2014年北京市、桂林市各季度平均气温统计图
| 第一季度 | 第二季度 | 第三季度 | 第四季度 | 年平均气温 |
北京市 | （_____） | （_____） | （_____） | （_____） | （_____） |
桂林市 | （_____） | （_____） | （_____） | （_____） | （_____） |
(2)两地平均气温最接近的是（_______）季度，平均气温差距最大的是（_________）季度。
(3)一年中，（________）市的平均气温比较高，（___________）市的平均气温变化较大。
