题目内容
一个四边形周长37厘米,四边形内有一点A,它到四条边的距离都是4.5厘米,那么,这个四边形面积是多少?
分析:画出一个四边形BCDG,找出点A,连接AG、AB、AC、AD得到四个三角形,△AGB、△ABC、△ACD、△ADG,四边形GBCD的面积等于这四个三角形的面积之和.
解答:解:连接AG、AB、AC、AD得到四个三角形,△AGB、△ABC、△ACD、△ADG,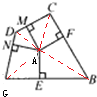
S△AGB=
×GB×AE,
S△ABC=
×BC×AF,
S△ACD=
×CD×AM,
S△ADG=
×DG×AN;
S四边形=S△AGB+S△ABC+S△ACD+S△ADG
而AE=AF=AM=AN=8厘米,
所以S四边形=
×AE×(GB+BC+CD+DG),
=
×4.5×37,
=83.25(平方厘米).
答:四边形GBCD的面积是83.25平方厘米.

S△AGB=
| 1 |
| 2 |
S△ABC=
| 1 |
| 2 |
S△ACD=
| 1 |
| 2 |
S△ADG=
| 1 |
| 2 |
S四边形=S△AGB+S△ABC+S△ACD+S△ADG
而AE=AF=AM=AN=8厘米,
所以S四边形=
| 1 |
| 2 |
=
| 1 |
| 2 |
=83.25(平方厘米).
答:四边形GBCD的面积是83.25平方厘米.
点评:把四边形ABCD分成四个三角形是解决此题的关键.

练习册系列答案
相关题目