题目内容
19.在一个面积为36平方厘米的等腰直角三角形中,有一个内接正方形,求正方形的面积.分析 如图:根据正方形对角线性质等腰直角三角形的性质作辅助虚线,图1,将等腰直角三角形分成9个相等的小三角形,正方形面积占了4份,即原面积的$\frac{4}{9}$,图2,将等腰直角三角形分成,4个相等的小三角形,正方形面积占了份,即原面积的$\frac{1}{2}$,据此解答.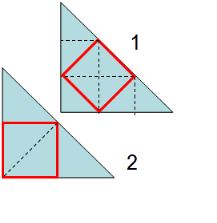
解答 解:36×$\frac{4}{9}$=16(平方厘米)
36×$\frac{1}{2}$=18(平方厘米)
答:正方形的面积是16平方厘米或18平方厘米.
点评 此题主要根据正方形对角线性质等腰直角三角形的性质,通过作辅助虚线,求出正方形与三角形面积之间的关系.

练习册系列答案
相关题目
9.用6,5,4,3,2,1,0组成的最小的七位数是( )
| A. | 1234560 | B. | 1023456 | C. | 6543210 |
3.列竖式计算(除法的要验算)
| 17.9×2.3 | 0.28×0.07 | 24.5×2.4 |
| 3.64÷52 | 19.76÷5.2 | 8.74÷0.38 |
10.一个数保留两位小数后的近似数是12.48,准确数不可能是( )
| A. | 12.4849 | B. | 12.47603 | C. | 12.48501 |

