Question

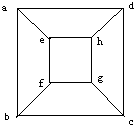如图8个顶点分别用a，b，c，d，e，f，g，h表示．每个顶点上的数是与它相邻三个顶点数和的

1

3

，求（a+b+c+d）-（d+e+f+g+h）的差．

Answer 1

分析：根据题意可知a=

1

3

（b+d+e），b=

1

3

（a+c+f），c=

1

3

（b+d+g），d=

1

3

（a+C+h），经过相加a+b+c+d=

1

3

（b+d+e）+

1

3

（a+c+f）+

1

3

（b+d+g）+

1

3

（a+C+h）得出a+b+c+d=e+f+g+h，进而解题．

解答：解：根据题意，可得
a=

1

3

（b+d+e），
b=

1

3

（a+c+f），
c=

1

3

（b+d+g），
d=

1

3

（a+C+h），
∴a+b+c+d=

1

3

（b+d+e）+

1

3

（a+c+f）+

1

3

（b+d+g）+

1

3

（a+C+h），
3（a+b+c+d）=2（a+b+c+d）+（e+f+g+h），
则a+b+c+d=e+f+g+h，
所以（a+b+c+d）-（e+f+g+h）=0，
答：（a+b+c+d）-（e+f+g+h）的差是0．

点评：完成本题关健是据已知条件为突破口，得出等量关系式，从而解决问题