题目内容
 9个小等边三角形拼成了如图的大等边三角形.每个小等边三角形中都填写了一个六位数,且有公共边的两个小等边三角形所填的六位数恰有一位不同.现已有小等边三角形中填好数.另外6个小三角形,共有
9个小等边三角形拼成了如图的大等边三角形.每个小等边三角形中都填写了一个六位数,且有公共边的两个小等边三角形所填的六位数恰有一位不同.现已有小等边三角形中填好数.另外6个小三角形,共有64
64
种填法.分析:如图:111122、A、F、E、112211依次相邻,而111122与112211有四位不同,所以由111122开台,每次只能变化一位,4次后变化112211,这样A、F、E的前2位都是1.同理,C、D、E的末两位都是1,A、B、C的中间两位也都是1.于是,A有111112或111121两种选择,C有121111或211111两种选择,C有121111或211111两种选择,E有111211或112111两种选择,当A和C确定后,有妨设A为111112,C为121111,于是B有121112或111111两种选择,同理,D、F各有两种选择.综上所述,A、B、C、D、E、F各有两种选择,根据排列组合的有知识可知,共有2×2×2×2×2×2=64种选择.


解答:解:如图,

由题意可知,A、B、C、D、E、F各有两种选择,根据排列组合的有知识可知,
共有2×2×2×2×2×2=64种选择.
故答案为:64.

由题意可知,A、B、C、D、E、F各有两种选择,根据排列组合的有知识可知,
共有2×2×2×2×2×2=64种选择.
故答案为:64.
点评:明确每个数字和其它两个数字不同的位数只有两个是完成本题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
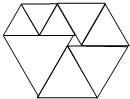 (2013?北京模拟)图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1厘米,这个六边形的周长是多少厘米?
(2013?北京模拟)图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1厘米,这个六边形的周长是多少厘米?
