Question

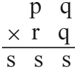（2012?武汉模拟）在这个乘法算式中，p、q、r、s各代表不同的数字．请问：p+q+r+s=

21

．

Answer 1

分析：两个两位数相乘积是3位数，那么，他们十位上的数相乘是不能进位的，
所以十位上的数p如果是1，则r可能是2、3、4、5、6、7、8、9；
如果p=2，则r=1、3、4；
如果p=3，则r=1、2；
如果p=4，则r=1、2；
如果p=5、6、7、8、9，r只能等于1；
又因为s不能为0，所以q也不能为0，；
因为得数是由3个相同的数组成，所以可能是111、222、333、444、555、666、777、888、999，
写出得数是这些数的符合的两位数乘两位数的算式，一一排除即可．

解答：解：由分析得出符合题意的算式是：
27×37=999，
所以p=2，q=7，r=3，s=9．
p+q+r+s=2+7+3+9=21．
故答案为：21．

点评：解决本题的关键是根据各个数位上数和得数特点进行推导．