题目内容
有一个形如13xy45z的七位数可以被792整除,则x、y、z这三个数字之和为
14
14
.分析:首先把729分解成,8,9,11的积的形式,然后考虑13xy45z这个数能被8整除时的条件,可以求出z,再考虑这个数能被9整除时的条件,能被11整除时的条件,根据所得的式子求出x,y的值.
解答:解:解:792=8×9×11,
13xy45z可以被8、9、11整除:
(1)可以被8整除时:
13xy45z=(13xy4×100+5z),
5z可以被8整除,
则z=6,(13xy456),
(2)可以被9整除时:
1+3+4+5+6+x+y可以被9整除,
即1+x+y可以被9整除,
则x+y=8或者x+y=17,
(3)可以被11整除时:
1+x+4+6=3+y+5或1+x+4+6=3+y+5(±11),
所以由x、y的范围,y=x+3,或者x=y+8联立几个条件,可得,
(x+y=8,x=y+8,x=8,y=0适用),(x+y=17,y=x+3,x=7,y=10不符合,放弃).
则13xy45z=1380456=792×1743.
所以,x+y+z=8+0+6=14
故答案为:14.
13xy45z可以被8、9、11整除:
(1)可以被8整除时:
13xy45z=(13xy4×100+5z),
5z可以被8整除,
则z=6,(13xy456),
(2)可以被9整除时:
1+3+4+5+6+x+y可以被9整除,
即1+x+y可以被9整除,
则x+y=8或者x+y=17,
(3)可以被11整除时:
1+x+4+6=3+y+5或1+x+4+6=3+y+5(±11),
所以由x、y的范围,y=x+3,或者x=y+8联立几个条件,可得,
(x+y=8,x=y+8,x=8,y=0适用),(x+y=17,y=x+3,x=7,y=10不符合,放弃).
则13xy45z=1380456=792×1743.
所以,x+y+z=8+0+6=14
故答案为:14.
点评:此题主要考查了一个七位数的数的整除性,做题时要考虑到一个数能被某个数整除时的条件,难度较大.

练习册系列答案
相关题目
 有一个转盘如图,随着转动,指针指向( )的可能性最大.
有一个转盘如图,随着转动,指针指向( )的可能性最大. 如图,在俄罗斯方块游戏中(出现的图案可进行顺时针、逆时针旋转;向左、向右平移),已拼好的图案如图所示,现又出现一个形如
如图,在俄罗斯方块游戏中(出现的图案可进行顺时针、逆时针旋转;向左、向右平移),已拼好的图案如图所示,现又出现一个形如 的方块正向下运动,你必须进行以下_______操作,才能拼成一个完整的矩形.( )
的方块正向下运动,你必须进行以下_______操作,才能拼成一个完整的矩形.( ) 有一个形状如图的零件,求它的体积和表面积.(单位:厘米).
有一个形状如图的零件,求它的体积和表面积.(单位:厘米).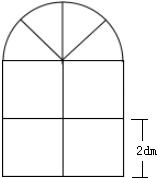 宿舍楼有一个窗户如图,上半部分是半圆形,下半部分是正方形.求这个窗户的周长和面积.(单位:分米)
宿舍楼有一个窗户如图,上半部分是半圆形,下半部分是正方形.求这个窗户的周长和面积.(单位:分米)