题目内容
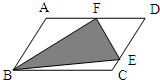 如图:平行四边形ABCD,已知F是AD的中点,DE=3EC,阴影部分的面积与空白部分的面积比是
如图:平行四边形ABCD,已知F是AD的中点,DE=3EC,阴影部分的面积与空白部分的面积比是7:9
7:9
.分析:假设整个平行四边形面积为1,因为△ABF的高和平行四边形的高相等,底是平行四边形的一半,且三角形求面积时要除以2,所以△ABF的面积是
÷2=
;因为△DFE的底是平行四边形的一半,高是平行四边形的
,所以△DFE的面积是
×
÷2=
;△EBC和平行四边形等底,但高是平行四边形的
,所以△EBC的面积是1×
÷2=
;由此求出空白部分的面积,进而求出阴影部分的面积,写出相应的比即可.
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 16 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
解答:解:设整个平行四边形面积为1,因为△ABF的高和平行四边形的高相等,底是平行四边形的一半,且三角形求面积时要除以2,
所以△ABF的面积是
÷2=
;
因为△DFE的底是平行四边形的一半,高是平行四边形的
,
所以△DFE的面积是
×
÷2=
;
△EBC和平行四边形等底,但高是平行四边形的
,
所以△EBC的面积是1×
÷2=
;
空白部分的面积:
+
+
=
,
则阴影部分面积为:1-
=
,
阴影部分的面积与空白部分的面积比是:
:
=7:9;
答:阴影部分的面积与空白部分的面积比是7:9.
故答案为:7:9.
所以△ABF的面积是
| 1 |
| 2 |
| 1 |
| 4 |
因为△DFE的底是平行四边形的一半,高是平行四边形的
| 3 |
| 4 |
所以△DFE的面积是
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 16 |
△EBC和平行四边形等底,但高是平行四边形的
| 1 |
| 4 |
所以△EBC的面积是1×
| 1 |
| 4 |
| 1 |
| 8 |
空白部分的面积:
| 1 |
| 4 |
| 3 |
| 16 |
| 1 |
| 8 |
| 9 |
| 16 |
则阴影部分面积为:1-
| 9 |
| 16 |
| 7 |
| 16 |
阴影部分的面积与空白部分的面积比是:
| 7 |
| 16 |
| 9 |
| 16 |
答:阴影部分的面积与空白部分的面积比是7:9.
故答案为:7:9.
点评:关键是利用空白的三个三角形与平行四边形的关系及三角形的面积公式分别求出三个空白的三角形的面积,进而解决问题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 如图,平行四边形ABCD的一边AB=8厘米,AB上的高等于3厘米,四边形EFOG的面积等于2平方厘米,则阴影部分的面积与平行四边形的面积之比是
如图,平行四边形ABCD的一边AB=8厘米,AB上的高等于3厘米,四边形EFOG的面积等于2平方厘米,则阴影部分的面积与平行四边形的面积之比是 如图,平行四边形ABCD,△EBA是直角三角形,AB=80cm,EB=70cm.已知阴影部分的面积比三角形EFH的面积大120cm2.求HB的长度.
如图,平行四边形ABCD,△EBA是直角三角形,AB=80cm,EB=70cm.已知阴影部分的面积比三角形EFH的面积大120cm2.求HB的长度. 如图,平行四边形中相邻两边AB:AD=4:3,如果AD=4.5厘米,那么AB的长度是
如图,平行四边形中相邻两边AB:AD=4:3,如果AD=4.5厘米,那么AB的长度是 (2010?邯山区)已知如图,平行四边形ABCD的边AB是半圆O的直径,边AB 的中点O是半圆的圆心,且半圆O的圆周经过点D,DO与AB垂直,垂足是点O,AB=6.求图中阴影部分的面积.
(2010?邯山区)已知如图,平行四边形ABCD的边AB是半圆O的直径,边AB 的中点O是半圆的圆心,且半圆O的圆周经过点D,DO与AB垂直,垂足是点O,AB=6.求图中阴影部分的面积. (2013?华亭县模拟)如图,平行四边形相邻的两条边AB与BC的长度的比是
(2013?华亭县模拟)如图,平行四边形相邻的两条边AB与BC的长度的比是