题目内容
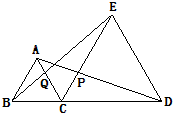如图，AB∥CE，AC∥DE，且CE=DE=2AB=2AC，则| CQ | CP |
1
1
．分析：我们连接AE，运用两个三角形高相等，面积的比等于它们底边的比，把PC，CQ分别用CE与CQ进行表示，在运用已知CE=DE=2AB=2AC，即可求出线段CQ与CP的比．
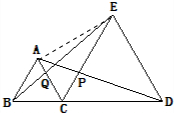
解答：解：因为AC∥DE，
所以S△ADE=S△CDE，S△APE=S△CPD，
又因为
=
，
=
=
=
，
所以
=
，
因为△EAC的边上的高和△CDE的边DE上的高相等，
所以
=
=
=
，
即，PC=
CE，
同理可得
=2，即CQ=
AC，
因为CE=DE=2AB=2AC，
所以
=
=
=1．
故答案为：1．
所以S△ADE=S△CDE，S△APE=S△CPD，
又因为
| PC |
| CE |
| S△CPD |
| S△CDE |
| PE |
| CE |
| S△APE |
| S△EAC |
| S△CPD |
| S△EAC |
| S△CPD |
| S△EAC |
所以
| PC |
| PE |
| S△EAC |
| S△CDE |
因为△EAC的边上的高和△CDE的边DE上的高相等，
所以
| PC |
| PE |
| S△EAC |
| S△CDE |
| AC |
| DE |
| 1 |
| 2 |
即，PC=
| 1 |
| 3 |
同理可得
| CQ |
| AQ |
| 2 |
| 3 |
因为CE=DE=2AB=2AC，
所以
| CQ |
| CP |
| ||
|
| 2AC |
| CE |
故答案为：1．
点评：本题运用两个三角形高相等，面积的比等于它们底边的比进行解答即可．
练习册系列答案
相关题目
如图，把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=6cm，DC=7cm，把三角板DCE绕点C顺时针旋转15°得到△D'CE'如图乙．这时AB与CD'相交于点O，D'E'与AB相交于点F．（1）求∠OFE'的度数；（2）求线段AD'的长．（3）若把三角形D'CE'绕着点C顺时针再旋转30°得△D''CE''，这时点B在△D''CE''的内部、外部、还是边上？证明你的判断．
如图，把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=6cm，DC=7cm，把三角板DCE绕点C顺时针旋转15°得到△D'CE'如图乙．这时AB与CD'相交于点O，D'E'与AB相交于点F．（1）求∠OFE'的度数；（2）求线段AD'的长．（3）若把三角形D'CE'绕着点C顺时针再旋转30°得△D''CE''，这时点B在△D''CE''的内部、外部、还是边上？证明你的判断．