Question

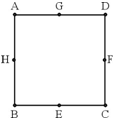从正方形的顶点及各边中点这八个点选取三个点，可组成

20

个等腰三角形．

Answer 1

分析：可用分类计数原理去做，按照选点的不同，分为三类，第一类：从正方形的四顶点中选三个点为顶点作三角形，第二类：从正方形的四边中点中选三个点为顶点作三角形，第三类：从正方形的四边中点中选两个点，四顶点中选一个点作三角形，或从正方形的四顶点中选两个点，从正方形的四边中点中选一个点作三角形，再把每类方法数相加，可得总的方法数．

解答：解：按题意可分三类．
第一类：从正方形的四顶点中选三个点为顶点作三角形，则全为等腰三角形，共有C₄³=4种．
第二类：从正方形的四边中点中选三个点为顶点作三角形，则全为等腰三角形，共有C₄³=4种，
第三类：从正方形的四边中点中选两个点，四顶点中选一个点作三角形，则每两个中点只能和它们所在边交点，或另两条边交点构成等腰三角形，或从正方形的四顶点中选两个点，从正方形的四边中点中选一个点作三角形，共有2C₄²=12种．
最后三类方法数相加得：4+4+12=20种．
故答案为：20．

点评：本题考查了分类原理在排列求和问题中的应用，注意分类依据，要做到不重不漏．