题目内容
如图，AF=3FB，FD=3EF，直角三角形ABC的面积是48平方厘米，求平行四边形EBCD和三角形AFD的面积。
由平行四边形特点可知：DE∥BC，
所以：
=
=
=
，
设，平行四边形的面积为x厘米2，S△ABC=48
=
=
=2，
=2，x=24，S△AFD=AF×DF÷2，S△ABC=AB×BC÷2，
=
，
=
，S△ABC=48厘米2，设S△AFD为y，
列出比例
=
=
?
=
，
=
，
16y=48×9，y=48×9÷16，y=27，
答：平行四边形EBCD和三角形AFD的面积各是24平方厘米，27平方厘米.
所以：
===，设，平行四边形的面积为x厘米2，S△ABC=48
===2，=2，x=24，S△AFD=AF×DF÷2，S△ABC=AB×BC÷2，=，=，S△ABC=48厘米2，设S△AFD为y，列出比例
==?=，=，16y=48×9，y=48×9÷16，y=27，
答：平行四边形EBCD和三角形AFD的面积各是24平方厘米，27平方厘米.
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
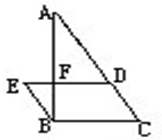如图，AF=3FB，FD=3EF，直角三角形ABC的面积是48平方厘米．求平行四边形EBCD和三角形AFD的面积．