Question

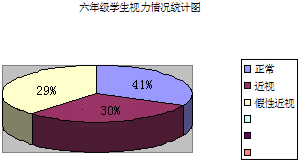下面是我校六年级学生视力情况统计图．
（1）视力正常的有82人，近视的有

60

人，假性近视的有

58

人．
（2）假性近视的同学比视力正常的同学少

24

人．
（3）视力正常的同学与视力非正常的人数比是

41：59

．

Answer 1

分析：（1）用视力正常的人数除以视力正常的人数占总人数的百分比（从统计图可以得知），即可求得六年级学生的总人数，再用总人数分别乘以近视以及假性近视的人数占总人数的百分比即可；
（2）用视力正常的人数减去假性近视的人数即可；
（3）用视力正常的同学的人数比视力非正常的人数（即近视的人数加上假性近视的人数），再化简成最简整数比即可．

解答：解：总人数：82÷41%=200（人），
近视的人数：200×30%=60（人）；
假性近视的人数：200×29%=58（人）；
答：近视的有60人，假性近视的有58人．

（2）82-58=24（人）；
答：假性近视的同学比视力正常的同学少24人．

（3）82：（60+58）
=82：118
=41：59；
答：视力正常的同学与视力非正常的人数比是41：59．
故答案为：（1）60，58；（2）24；（3）41：59．

点评：此题主要考查的是如何从扇形统计图中获取信息，然后再根据信息进行分析、计算、解决问题的能力．