题目内容
 如图所示,正六边形ABCDEF的面积是36平方厘米,AG=
如图所示,正六边形ABCDEF的面积是36平方厘米,AG=| 1 |
| 3 |
| 1 |
| 2 |
9
9
平方厘米.分析:如图所示,连接GC、GD、AD,则三角形DGH和三角形HGC的面积相等,三角形BCG和三角形ADG的面积相等,所以四边形GHCB的面积等于四边形ADHG的面积,又因四边形ABCD的面积等于六边形的面积的一半,于是即可求出四边形BCHG的面积.


解答:解:连接GC、GD、AD,则三角形DGH和三角形HGC的面积相等,
三角形BCG和三角形ADG的面积相等,
所以四边形GHCB的面积等于四边形ADHG的面积,
又因四边形ABCD的面积等于六边形的面积的一半,
则四边形BCHG的面积为:36×
×
=9(平方厘米);
答:四边形BCHG的面积是9平方厘米.
故答案为:9.
三角形BCG和三角形ADG的面积相等,
所以四边形GHCB的面积等于四边形ADHG的面积,
又因四边形ABCD的面积等于六边形的面积的一半,
则四边形BCHG的面积为:36×
| 1 |
| 2 |
| 1 |
| 2 |
答:四边形BCHG的面积是9平方厘米.
故答案为:9.
点评:解答此题关键是明白:四边形GHCB的面积等于四边形ADHG的面积.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
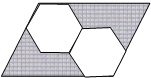 如图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的( )
如图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的( )A、
| ||
B、
| ||
C、
| ||
D、
|
 好学的小明学了量角器的使用后,在家很快测出了正六边形花盆一个角的大小,如图所示,则这个角的大小是( )
好学的小明学了量角器的使用后,在家很快测出了正六边形花盆一个角的大小,如图所示,则这个角的大小是( )| A、60度 | B、120度 | C、110度 |
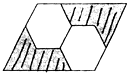 如图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的( )
如图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的( ) 如图所示,在正六边形A周围画出6个同样的正六边形(阴影部分),围成第1圈;在第1圈外面再画出12个同样的正六边形,围成第2圈;….按这个方法继续画下去,当画完第9圈时,图中共有
如图所示,在正六边形A周围画出6个同样的正六边形(阴影部分),围成第1圈;在第1圈外面再画出12个同样的正六边形,围成第2圈;….按这个方法继续画下去,当画完第9圈时,图中共有 如图所示,在正六边形A周围画出6个同样的正六边形(阴影部分),围成第1圈;在第1圈外面再画出12个同样的正六边形,围成第2圈;….按这个方法继续画下去,当画完第9圈时,图中共有________个与A相同的正六边形.
如图所示,在正六边形A周围画出6个同样的正六边形(阴影部分),围成第1圈;在第1圈外面再画出12个同样的正六边形,围成第2圈;….按这个方法继续画下去,当画完第9圈时,图中共有________个与A相同的正六边形.