Question

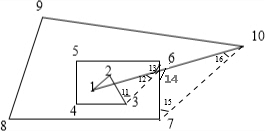
如图，标有记号的十个角之和是

720

度．

Answer 1

分析：连接∠3和∠6的顶点，∠7和∠10的顶点，如图，根据三角形的内角和定理，平角的定义以及三角形的一个外角等于跟它不相邻的两个内角之和，则可得∠1+∠2=∠11+∠12；∠13=∠14，由此可得：
根据五边形的内角和是540度可得：∠1+∠2+∠3+∠4+∠5+∠6=540-∠13；
根据四边形内角和是360度可得：∠7+∠8+∠9+∠10=360-∠15-∠16；
所以：∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10=540-∠13+360-∠15-∠16=540+360-（∠13+∠15+∠16）=900-（∠13+∠15+∠16），因为∠13=∠14，所以∠13+∠15+∠16=∠14+∠15+∠16=180度，由此代入即可求出这10个角的度数之和．

解答：解：连接∠3和∠6的顶点，∠7和∠10的顶点，根据题干分析可得：
∠1+∠2+∠3+∠4+∠5+∠6=540-∠13；
∠7+∠8+∠9+∠10=360-∠15-∠16；
所以：∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10，
=540-∠13+360-∠15-∠16，
=540+360-（∠13+∠15+∠16），
=900-（∠13+∠15+∠16），
因为∠13=∠14，所以∠13+∠15+∠16=∠14+∠15+∠16=180度，
所以∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10=900-180=720（度）；
答：这10个角的度数之和是720度．
故答案为：720．

点评：此题考查多边形内角和定理的灵活应用，解答此题的关键是把这10个角转化到多边形中利用内角和定理解答．