题目内容
 如图所示,正方形ABCD的面积为2平方厘米,它的对角线长AC=2厘米,扇形ACD是以D为圆心,以AD为半径的圆面积的一部分,那么阴影部分的面积是
如图所示,正方形ABCD的面积为2平方厘米,它的对角线长AC=2厘米,扇形ACD是以D为圆心,以AD为半径的圆面积的一部分,那么阴影部分的面积是π-2
π-2
平方厘米.分析:由图意可织:阴影部分的面积=半圆的面积-三角形ABC的面积+(S扇ACD-S△ACD),由正方形的面积是2平方厘米可求其边长,又因ABCD是正方形,AC=2厘米,将数据代入等式即可求得阴影部分的面积.
解答:解:设正方形的边长为a,圆的半径=2÷2=1厘米,
则a2=2,
阴影部分的面积=半圆的面积-三角形ABC的面积+(S扇ACD-S△ACD),
=
π×12-
a2+
π×a2-
a2,
=
π-1+
π-1,
=π-2(平方厘米);
答:那么阴影部分的面积是π-2平方厘米.
故答案为:π-2.
则a2=2,
阴影部分的面积=半圆的面积-三角形ABC的面积+(S扇ACD-S△ACD),
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=π-2(平方厘米);
答:那么阴影部分的面积是π-2平方厘米.
故答案为:π-2.
点评:解决此题的关键是明白阴影部分的面积=半圆的面积-三角形ABC的面积+(S扇ACD-S△ACD).

练习册系列答案
相关题目
 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形. 如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是
如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是 如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?
如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?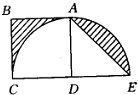 如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?
如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米? 如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是________平方厘米.
如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是________平方厘米.