题目内容
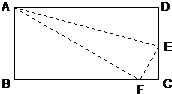 (2012?宜宾县模拟)如图,长方形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,则∠DAE=
(2012?宜宾县模拟)如图,长方形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,则∠DAE=15
15
.分析:根据长方形ABCD沿AE折叠,使D点落在BC边上的F点处,知道∠DAE=
∠DAF,再根据在直角三角形的两个锐角的和是90度,即可求出答案.
| 1 |
| 2 |
解答:解:长方形ABCD沿AE折叠,使D点落在BC边上的F点处,
所以AE垂直平分DF,AD=AF,
∠DAE=
∠DAF,
又因为,∠BAF=60°,∠BAD=90°,
所以,∠DAF=∠BAD-∠BAF=30°,
∠DAE=15°;
故答案为:15°.
所以AE垂直平分DF,AD=AF,
∠DAE=
| 1 |
| 2 |
又因为,∠BAF=60°,∠BAD=90°,
所以,∠DAF=∠BAD-∠BAF=30°,
∠DAE=15°;
故答案为:15°.
点评:解答此题的关键是,根据折叠的方式,找出哪些量发生变化,哪些量没有发生变化,即可解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目