题目内容
如图，AB=CD=EF=2，BC=DE=4，∠B=∠C=∠D=∠E=90°，AF的长为________．
10
分析：延长FE至G作AG⊥GF，则AG=BC+DE=4+4=8，GF=AB+CD+EF=2+2+2=6，在直角三形AGF中，根据勾股定理即可求得AF的长．
解答：如图，
延长FE至G作AG⊥GF，则AG=BC+DE=4+4=8，GF=AB+CD+EF=2+2+2=6，在直角三形AGF中AF=
=
=10；
故答案为：10．
点评：解答此题的关键是作辅助线，用勾股定理解答，小学生解答比较困难．
分析：延长FE至G作AG⊥GF，则AG=BC+DE=4+4=8，GF=AB+CD+EF=2+2+2=6，在直角三形AGF中，根据勾股定理即可求得AF的长．
解答：如图，
延长FE至G作AG⊥GF，则AG=BC+DE=4+4=8，GF=AB+CD+EF=2+2+2=6，在直角三形AGF中AF=
==10；故答案为：10．
点评：解答此题的关键是作辅助线，用勾股定理解答，小学生解答比较困难．
练习册系列答案
阅读快车系列答案
相关题目
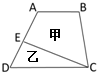如图所示，E是AD边上的中点，CE把梯形分成甲、乙两个部分，面积比是10：7，上底AB与下底CD的长度比是
如图，AB=CD=EF=2，BC=DE=4，∠B=∠C=∠D=∠E=90°，AF的长为
如图梯形中的E是AD中点，线段CE把梯形分成甲、乙两个部分，面积比是10：7．那么梯形的上底AB与下底CD的长度比AB：CD=