Question

设半径为10厘米的球中有一个棱长为整数（厘米）的正方体，则该正方体的棱长最大等于多少？

Answer 1

分析：画出图形，见下图，球的内接正方形ABCD-A₁B₁C₁D₁的顶点在球面上，它的（体）对角线AC₁就是球的直径，即AC₁=2×10=20（厘米）．然后由图的对称性以及勾股定理解决问题．

解答：解：

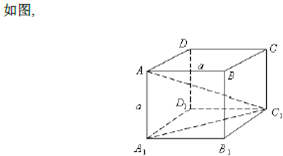
球的内接正方形ABCD-A₁B₁C₁D₁的顶点在球面上，它的（体）对角线AC₁就是球的直径，即AC₁=2×10=20（厘米）．
由图的对称性，可知∠AA₁C₁=90°，∠A₁B₁C₁=90°．
设正方形的棱长为a，即AA₁=A₁B₁=B₁C₁=a，连续用勾股定理两次，得到：
A₁C₁²=2a²，AC₁²=AA₁²+A1C₁²+3a²，
则3a²=20²=400，a²=

400

3

=133

1

3

．
显然，只要一个正方体的棱长a为整数，满足a²≤133，那么这个正方体一定可以放入球中，因为11²=121＜133＜144=12²．故所求的棱长为整数的正方体的最大棱长等于11厘米．
答：该正方体的棱长最大等于11厘米．

点评：此题根据图形特点，运用了图的对称性以及勾股定理解决问题．