题目内容
如图,以下是大小相同的五个正六边形,若其阴影部分的面积依次记为a,b,c,d,e,试判断a,b,c,d,e的大小关系.


分析:本题通过运用三角形的面积公式进行推理计算比较.通过推理发现阴影a、b、d的面积相等都是正六边形的面积的
,c、e的面积是正六边形面积的
,因此a、b、d相等,ce相等a、b、d小于c、e.
| 1 |
| 2 |
| 2 |
| 3 |
解答:解:由下图可知,

△BCD与△OCD面积相等,
所以阴影a=3△OCD=
正六边形面积,
b=3△OCD=
正六边形面积,
d=3△OCD=
正六边形面积,
所以a=b=d,
由此可知c=正六边形面积-2△BCD=4△OCD=
正六边形面积,

因为HI是AE的三等分点,MN是AC的三等分点,GI是FD的三等分点,NK是BD的三等分点KG是CE的三等分点,HI是EA的三等分点.
所以.△AMB,△AMH,△AHF,△AMB,△BMN,△BNC,△CNK,△CKD,△DKG,△DGE,△EGI,△EIF面积都是相等的,去掉六个小三角形的面积,阴影部分的面积e=4△OCD=
正六边形的面积,
所以c=e,
因此:a=b=d小于c=e,

△BCD与△OCD面积相等,
所以阴影a=3△OCD=
| 1 |
| 2 |
b=3△OCD=
| 1 |
| 2 |
d=3△OCD=
| 1 |
| 2 |
所以a=b=d,
由此可知c=正六边形面积-2△BCD=4△OCD=
| 2 |
| 3 |

因为HI是AE的三等分点,MN是AC的三等分点,GI是FD的三等分点,NK是BD的三等分点KG是CE的三等分点,HI是EA的三等分点.
所以.△AMB,△AMH,△AHF,△AMB,△BMN,△BNC,△CNK,△CKD,△DKG,△DGE,△EGI,△EIF面积都是相等的,去掉六个小三角形的面积,阴影部分的面积e=4△OCD=
| 2 |
| 3 |
所以c=e,
因此:a=b=d小于c=e,
点评:本题要借助正六边形的面积进行计算,有些地方需要用初中知识进行解答会更好.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
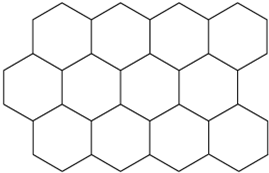 卡纸上编号1~4的图形均是由数量不等的相同大小的正六边形组成的.请完成以下问题:
卡纸上编号1~4的图形均是由数量不等的相同大小的正六边形组成的.请完成以下问题: