题目内容
求阴影部分面积


分析:(1)阴影部分的面=正方形的面积-圆的面积,又因正方形的边长等于圆的直径,据此即可得解;
(2)由题意可知:阴影部分的面积=半径为1厘米的圆的面积-直径为1厘米的圆的面积;
(3)阴影部分的面积=半径为4厘米的圆的面积+边长为4厘米的正方形面积;
(4)阴影部分的面积=正方形的面积-
圆的面积,三角形AOB的面积已知,则可以求出半径的平方值,从而问题得解;
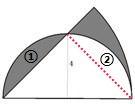
(5)如图所示,阴影①和空白②的面积相等,则阴影部分的面积就等于圆心角为45°的扇形的面积-等腰直角三角形的面积;
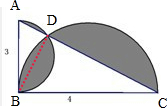
(6)如图所示,阴影部分的面积=(小半圆的面积-三角形ABD的面积)+(大半圆的面积-三角形BDC的面积),也就等于两个半圆的面积和减去三角形的面积,据此即可得解;
(7)环形的面积已知,依据环形的面积S=π(R2-r2),即可求出(R2-r2)的值,又因阴影部分的面积=大正方形的面积-小正方形的面积=(R2-r2),
于是据此即可求出阴影部分的面积;
(8)阴影部分的面积就等于圆心角为45°的扇形的面积,据此即可得解;
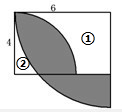
(9)如图所示,阴影部分的面积=以6厘米为半径的
圆的面积-空白①的面积,而空白①的面积=长方形的面积-以6厘米为半径的
圆的面积,据此即可得解;
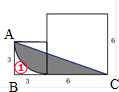
(10)如图所示,阴影部分的面积=三角形ABC的面积-空白①的面积,而空白①的面积=小正方形的面积-以3厘米为半径的
圆的面积,据此即可得解;
(2)由题意可知:阴影部分的面积=半径为1厘米的圆的面积-直径为1厘米的圆的面积;
(3)阴影部分的面积=半径为4厘米的圆的面积+边长为4厘米的正方形面积;
(4)阴影部分的面积=正方形的面积-
| 1 |
| 4 |
(5)如图所示,阴影①和空白②的面积相等,则阴影部分的面积就等于圆心角为45°的扇形的面积-等腰直角三角形的面积;

(6)如图所示,阴影部分的面积=(小半圆的面积-三角形ABD的面积)+(大半圆的面积-三角形BDC的面积),也就等于两个半圆的面积和减去三角形的面积,据此即可得解;

(7)环形的面积已知,依据环形的面积S=π(R2-r2),即可求出(R2-r2)的值,又因阴影部分的面积=大正方形的面积-小正方形的面积=(R2-r2),
于是据此即可求出阴影部分的面积;
(8)阴影部分的面积就等于圆心角为45°的扇形的面积,据此即可得解;
(9)如图所示,阴影部分的面积=以6厘米为半径的
| 1 |
| 4 |
| 1 |
| 4 |

(10)如图所示,阴影部分的面积=三角形ABC的面积-空白①的面积,而空白①的面积=小正方形的面积-以3厘米为半径的
| 1 |
| 4 |

解答:解:(1)20×20-3.14×(20÷2)2,
=400-314,
=86(平方厘米);
答:阴影部分的面积是86平方厘米.
(2)1÷2=0.5(厘米),
3.14×(12-0.52),
=3.14×(1-0.25),
=3.14×0.75,
=2.355(平方厘米);
答:阴影部分的面积是2.355平方厘米.
(3)3.14×42+4×4,
=50.24+16,
=66.24(平方厘米);
答:阴影部分的面积是66.24平方厘米.
(4)因为三角形的面积为5平方厘米,
则r2=10,
所以阴影部分的面积为:
5×2-
×3.14×10,
=10-7.85,
=2.15(平方厘米);
答:阴影部分的面积是2.15平方厘米.
(5)
×3.14×(4×2)2-4×2×4÷2,
=
×3.14×64-16,
=25.12-16,
=9.12(平方厘米);
答:阴影部分的面积是9.12平方厘米.
(6)3.14×(3÷2)2÷2+3.14×(4÷2)2÷2-3×4÷2,
=3.5325+6.28-6,
=3.8125(平方厘米);
答:阴影部分的面积是3.8125平方厘米.
(7)设大圆的半径为R,小圆的半径为r,
则π(R2-r2)=125.6,
R2-r2=125.6÷3.14=40,
阴影部分的面积=R2-r2,
所以阴影部分的面积是40平方厘米.
答:阴影部分的面积是40平方厘米.
(8)
×3.14×52,
=
×3.14×25,
=9.8125(平方厘米);
答:阴影部分的面积是9.8125平方厘米.
(9)3.14×62×
-(6×4-3.14×42×
),
=28.26-(24-12.56),
=28.26-11.44,
=16.82(平方厘米);
答:阴影部分的面积啊16.82平方厘米.
(10)(3+6)×3÷2-(3×3-3.14×32×
),
=13.5-(9-7.065),
=13.5-1.935,
=11.565(平方厘米);
答:阴影部分的面积是11.565平方厘米.
=400-314,
=86(平方厘米);
答:阴影部分的面积是86平方厘米.
(2)1÷2=0.5(厘米),
3.14×(12-0.52),
=3.14×(1-0.25),
=3.14×0.75,
=2.355(平方厘米);
答:阴影部分的面积是2.355平方厘米.
(3)3.14×42+4×4,
=50.24+16,
=66.24(平方厘米);
答:阴影部分的面积是66.24平方厘米.
(4)因为三角形的面积为5平方厘米,
则r2=10,
所以阴影部分的面积为:
5×2-
| 1 |
| 4 |
=10-7.85,
=2.15(平方厘米);
答:阴影部分的面积是2.15平方厘米.
(5)
| 45 |
| 360 |
=
| 1 |
| 8 |
=25.12-16,
=9.12(平方厘米);
答:阴影部分的面积是9.12平方厘米.
(6)3.14×(3÷2)2÷2+3.14×(4÷2)2÷2-3×4÷2,
=3.5325+6.28-6,
=3.8125(平方厘米);
答:阴影部分的面积是3.8125平方厘米.
(7)设大圆的半径为R,小圆的半径为r,
则π(R2-r2)=125.6,
R2-r2=125.6÷3.14=40,
阴影部分的面积=R2-r2,
所以阴影部分的面积是40平方厘米.
答:阴影部分的面积是40平方厘米.
(8)
| 45 |
| 360 |
=
| 1 |
| 8 |
=9.8125(平方厘米);
答:阴影部分的面积是9.8125平方厘米.
(9)3.14×62×
| 1 |
| 4 |
| 1 |
| 4 |
=28.26-(24-12.56),
=28.26-11.44,
=16.82(平方厘米);
答:阴影部分的面积啊16.82平方厘米.
(10)(3+6)×3÷2-(3×3-3.14×32×
| 1 |
| 4 |
=13.5-(9-7.065),
=13.5-1.935,
=11.565(平方厘米);
答:阴影部分的面积是11.565平方厘米.
点评:当阴影部分的面积不能直接求出时,需要认真观察,利用图形的割补方法,将阴影部分进行重组,利用规则图形的面积和或差求解.

练习册系列答案
相关题目


 图形面积计算,如图,长方形的长为6厘米,宽为4厘米,求阴影部分面积.
图形面积计算,如图,长方形的长为6厘米,宽为4厘米,求阴影部分面积. 长方形BEOF,AEOH,HDGO的面积分别是5,6,7,求阴影部分面积是
长方形BEOF,AEOH,HDGO的面积分别是5,6,7,求阴影部分面积是 如图中等腰三角形的底角是45°,虚线表示扇形的半径,也是等腰三角形的高.求阴影部分面积.
如图中等腰三角形的底角是45°,虚线表示扇形的半径,也是等腰三角形的高.求阴影部分面积.