Question

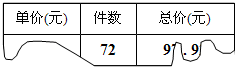有一张残缺的发票如图，那么单价是

97.92

元．

Answer 1

分析：首先根据凡能被9除尽的数，它各个位上的数加起来也能被9整除，假设十位的数为x，百分位的数为y，分析得出x+y值，结合数的整除性可以得出x的值．

解答：解：凡能被9除尽的数，它各个位上的数加起来也能被9整除，比如495÷9=55，4+9+5=18，18能被9整除．
所以x+9+9+y应该能被9整除．x的取值范围是1-9，y的取值范围是0-9，
所以x+9+9+y的最小值是1+9+9+0=19，最大值是9+9+9+9=36．
在19-36之间的数里面，能被9整除的只有27、36．即x+y=9或18．
所以x9.9y有可能是：
99.90，98.91，97.92，96.93，95.94，94.95，93.96，92.97，91.98，90.99，99.99．
在价格里面，分应该是最小的，而x9.9y不仅要能被9除尽，还要能被8除尽，
所以y如果是单数，会出现比分更小的单位，不符合实际，所以排除y是单数的情况，剩下：
99.90，97.92，95.94，93.96，91.98，．
它们除以72，分别得：
99.90÷72=1.3875，
97.92÷72=1.36，
95.94÷72=1.3325，
93.96÷72=1.305，
91.98÷72=1.2775，
显然，除97.92外，其他都会出现单价有比分更小的单位的情况，所以只有97.92符合实际，
故答案为：97.92．

点评：解答此题的关键是能被72整除，即能被8、9整除，然后根据能被8和9整除的数的特征进行分析、解答即可．