Question

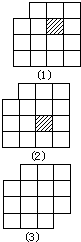三个图形都是从4×4的正方形分别剪去两个1×1的小方格得到的，问可否把它们分别剪成1×2的七个小矩形？

Answer 1

分析：先对4×4的正方形黑白相间的涂色（如图），这道题的实际问题是问7个1×2矩形能否分别复盖剪去A、B，剪去A、C，剪去A、D的三个正方形．若7个1×2矩形可以复盖剪残的正方形，因为每个1×2矩形均可盖住一个白格和一个黑格，所以棋盘的白格与黑格数目应该相等．都是7个．而剪去A格和C格的正方形（2）有5个白格8个黑格，剪去A、D的正方形（3）有5个白格8个黑格，因此这两个剪损的正方形均不能被7个1×2矩形复盖，也就不能剪成7个1×2的矩形．但正方形（1）中分别有7个黑格，7个白格，它能被7个1×2矩形覆盖．

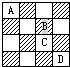
解答：解：如图，

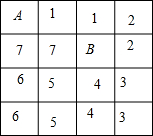
因为每个1×2矩形均可盖住一个白格和一个黑格，若7个1×2矩形可以复盖剪残的正方形，
所以棋盘的白格与黑格数目应该相等．都是7个．
而剪去A格和C格的棋盘（2）有5个白格8个黑格，剪去A、D的棋盘（3）有5个白格8个黑格，
因此这两个剪损的棋盘均不能被7个1×2矩形复盖，也就不能剪成7个1×2的矩形．
正方形（1）中分别有7个黑格，7个白格，它能被7个1×2矩形覆盖．下面给出一种剪法：

点评：完成本题的关健是要明确若要被7个1×2矩形覆盖，正方形中的黑格和白格必须是相等的．