Question

在长260厘米，宽150厘米的台球桌上，有A、B、C、D、E、F6个球袋，其中AB=EF=130厘米，现在从A处沿45°方向打出一球，如图所示，碰到桌边后又沿45°方向弹出，当再碰到桌边时，仍沿45°方向弹出，此继续下去，假如球可以一直运动，直至落入某个袋中为止，那么它将落入

E

袋．

Answer 1

分析：设想把台球桌子以它的宽所在的边为轴向右作对称图形，一直作下去，这样球在宽边上的弹射可认为被拉直到长边上去了，因而只考虑球在两条长边上的弹射情况．如下图，由于知AFAF=CD=150厘米，根据等腰三角形的性质因此球在两条横边上的弹击点与初始位置A（或F）点的距离总是150的倍数，而相邻两袋之间的距离为130厘米，所以当弹射进行到某个位置时，弹击点与初始位置A（或F）点的距离恰好也是130的倍数时，此时球将落入那个弹击点所在的袋中．据此，我们只需求出150与130的最小公倍数即可．　　

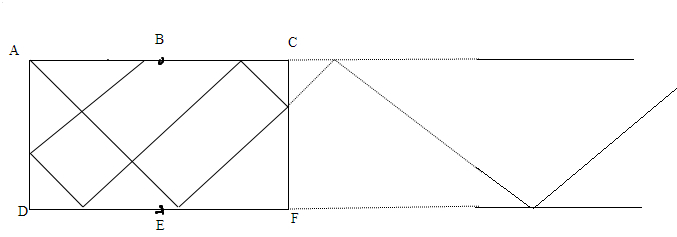
解答：解：150=3×5×2×5，
130=13×2×5，
所以，150与130的最小公倍数是2×5×13×3×5=1950．
下面再判断一下弹击点在ACA C边上还是在FDF D边上．因为A CAC边上，弹击点与A 的距离都是150的偶数倍；而FDF D边上，弹击点与F反射点的距离都是150的奇数倍，又1950=13×150，因此弹击点应在F D边上，且是第13个（包括A C边上）弹击点．下面再考虑是F D边上的哪个球袋．由于1950=15×130=7×260+130，这说明弹射过程经过了7个台球桌后，在经过第8个台球桌时，球落入F D边上的中间哪个球袋，即是E袋．
答：球最后落在EE袋中．

点评：灵活运用最小公倍数解决实际问题，培养了学生的动手操作能力．