题目内容
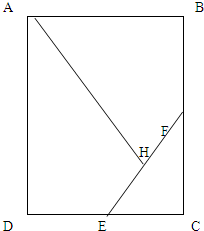如图，在长方形ABCD中，已知E是DC的中点，F是BC的中点，H是FE的中点，AB=12分米，BC=20分米，那么三角形AHE的面积是多少？（提示：连接AE、AF）分析：连接AE、AF，因为H是FE的中点，所以只要求出三角形AEF的面积即可求出三角形AHE的面积，观察图形可知，三角形AEF的面积等于长方形的面积减去周围三个直角三角形的面积，由此利用已知边长和面积公式即可解答问题．
解答：解：连接AE、AF，因为E是DC的中点，F是BC的中点，AB=12分米，BC=20分米，
所以DE=EC=12÷2=6（分米），
BF=FC=20÷2=10（分米），
所以三角形AEF的面积是：12×20-20×6÷2-10×6÷2-10×12÷2，
=240-60-30-60，
=90（平方分米），
因为H是FE的中点，
所以三角形AHE的面积是90÷2=45（平方分米），
答：三角形AHE的面积是45平方分米．
所以DE=EC=12÷2=6（分米），
BF=FC=20÷2=10（分米），
所以三角形AEF的面积是：12×20-20×6÷2-10×6÷2-10×12÷2，
=240-60-30-60，
=90（平方分米），
因为H是FE的中点，
所以三角形AHE的面积是90÷2=45（平方分米），
答：三角形AHE的面积是45平方分米．
点评：此题考查了长方形、三角形的面积公式，以及高一定时三角形的面积与底成正比例的性质的灵活应用．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
两个形状和大小都一样的直角三角形△ABC和△DEF，如图放置，它们的面积都是2003平方厘米，而每一个三角形的顶点恰好都落在另一个三角形的斜边上．这两个直角三角形的重叠部分是一个长方形，那么四边形ADEC的面积为
（2008?宝应县）（1）如表每小方格面积1平方厘米，先在图中画一个长4cm，宽3cm的长方形，再在长方形中画一个最大的圆，求出圆的面积．
（1）如表每小方格面积1平方厘米，先在图中画一个长4cm，宽3cm的长方形，再在长方形中画一个最大的圆，求出圆的面积．