Question

Answer 1

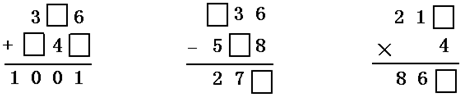
分析：根据加法和除法竖式计算的方法逐步推算即可．
（1）个位上：6+□=11，可知□填4，向十位进一，十位上：4+1+□=10，可知□填6，向百位进一，百位上：3+□+1=10，可知□填6，从而可以列出竖式；
（2）根据竖式中，被减数个位位是6，减数个位是8，不够减，得向十位借1当10，与个位合起来是16，16-8=8，故差的个位应是8；被减数的十位还剩2，差的十位上是7，由此可知十位上不够减，要向百位借一当十，12-□=7，可得出减数十位上填5；由差的百位2与除数的百位5，及十位上借的1合起来就是被减数百位上的数，所以2+5+1=8，可得出被减数的百位上填8；
（3）根据竖式可知：4乘以第一个因数百位4得出积的百位正好是4，4再乘以第一个因数十位上1得出4，与积的十位上6相差2，说明是个位上的数与4相乘应是二十几，就想4乘几是二十几的，由此得出第一个因数的个位可以是5、6、7，相对应的积是0、4、8．

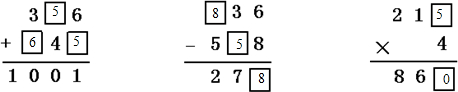
解答：解：（1）个位上：6+□=11，可知□填4，向十位进一，
十位上：4+1+□=10，可知□填6，向百位进一，
百位上：3+□+1=10，可知□填6，
由此可得竖式：
（2）根据竖式中，被减数个位位是6，减数个位是8，不够减，得向十位借1当10，与个位合起来是16，16-8=8，故差的个位应是8；
被减数的十位还剩2，差的十位上是7，由此可知十位上不够减，要向百位借一当十，12-□=7，可得出减数十位上填5；
由差的百位2与除数的百位5，及十位上借的1合起来就是被减数百位上的数，所以2+5+1=8，可得出被减数的百位上填8；
由此可得竖式：
（3）根据竖式可知：4乘以第一个因数百位4得出积的百位正好是4，4再乘以第一个因数十位上1得出4，与积的十位上6相差2，说明是个位上的数与4相乘应是二十几，就想4乘几是二十几的，由此得出第一个因数的个位可以是5、6、7，相对应的积是0、4、8．
由此可得竖式：

点评：根据题意，注意加法的进位加法，减法的退位减法，乘法竖式计算方法，就可以推出结果．