题目内容
 如图,甲三角形比乙三角形的面积大6平方厘米,求DE的长.
如图,甲三角形比乙三角形的面积大6平方厘米,求DE的长.
解:(4×6+6)×2÷6-4,
=(24+6)×2÷6-4,
=30×2÷6-4,
=10-4,
=6(厘米).
答:DE的长是6厘米.
分析:根据题意,三角形DEF比三角形ABF面积大6平方厘米,那么三角形BCE的面积比长方形ABCD的面积大6平方厘米,可利用长方形的面积加上6平方厘米就是三角形的BCE的面积,再根据三角形的面积公式计算出高CE的长,DE=CE-CD,列式解答即可得到答案.
点评:解答此题的关键是确定三角形BCE的面积比长方形ABCD的面积大6平方厘米,然后再计算三角形BCE的高CE的长,最后再计算DE的长即可.
=(24+6)×2÷6-4,
=30×2÷6-4,
=10-4,
=6(厘米).
答:DE的长是6厘米.
分析:根据题意,三角形DEF比三角形ABF面积大6平方厘米,那么三角形BCE的面积比长方形ABCD的面积大6平方厘米,可利用长方形的面积加上6平方厘米就是三角形的BCE的面积,再根据三角形的面积公式计算出高CE的长,DE=CE-CD,列式解答即可得到答案.
点评:解答此题的关键是确定三角形BCE的面积比长方形ABCD的面积大6平方厘米,然后再计算三角形BCE的高CE的长,最后再计算DE的长即可.

练习册系列答案
相关题目
 (2012?绍兴县)在如图中,平行四边形的面积是20平方厘米,图中甲、乙、丙三个三角形的面积比是
(2012?绍兴县)在如图中,平行四边形的面积是20平方厘米,图中甲、乙、丙三个三角形的面积比是 如图,平行四边形的面积是30平方分米,甲、乙、丙三个三角形的面积的比是( )
如图,平行四边形的面积是30平方分米,甲、乙、丙三个三角形的面积的比是( )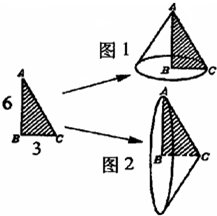
 如图中,平行四边形的面积是20平方米,则图中甲、乙、丙三个三角形的面积比是( )
如图中,平行四边形的面积是20平方米,则图中甲、乙、丙三个三角形的面积比是( ) 平行四边形被分成了甲、乙、丙三个三角形(如图).AE=15,ED=10,请分别写出甲与乙、乙与丙和甲与丙的面积的最简整数比.
平行四边形被分成了甲、乙、丙三个三角形(如图).AE=15,ED=10,请分别写出甲与乙、乙与丙和甲与丙的面积的最简整数比.