题目内容
 如图,三角形ABC是等腰直角三角形,斜边AB=12厘米,MN是BC的
如图,三角形ABC是等腰直角三角形,斜边AB=12厘米,MN是BC的| 1 |
| 3 |
| 1 |
| 4 |
分析:如图所示,作三角形ABC斜边上的高CE,又因等腰直角三角形斜边上的高等于斜边的一半,则CE=
AB=6厘米,于是可以求出三角形ABC的面积,又因AP=
AC,则PC=
AC,所以三角形PCB的面积等于三角形ABC的面积的
,又因MN=
BC,则三角形PMN的面积等于三角形PCD的面积的
,据此即可求出阴影部分的面积.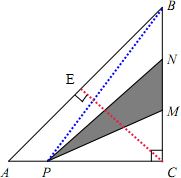
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |

解答:解:据分析可知:CE=
AB=6厘米,
则三角形ABC的面积为:
×12×(12÷2)=36平方厘米,
又因AP=
AC,则PC=
AC,
所以三角形PCB的面积等于三角形ABC的面积的
,即三角形PCB的面积为
×36=27平方厘米,
又因MN=
BC,则三角形PMN的面积等于三角形PCD的面积的
,
即三角形PMN的面积为27×
=9平方厘米.
答:三角形PMN的面积是9平方厘米.
| 1 |
| 2 |
则三角形ABC的面积为:
| 1 |
| 2 |
又因AP=
| 1 |
| 4 |
| 3 |
| 4 |
所以三角形PCB的面积等于三角形ABC的面积的
| 3 |
| 4 |
| 3 |
| 4 |
又因MN=
| 1 |
| 3 |
| 1 |
| 3 |
即三角形PMN的面积为27×
| 1 |
| 3 |
答:三角形PMN的面积是9平方厘米.
点评:解答此题的主要依据是:等腰直角三角形斜边上的高等于斜边的一半,等高不等底的三角形的面积比等于对应底边的比.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图:三角形ABC是直角三角形,AC是圆的半径且AC=10cm.阴影Y的面积比阴影X的面积小32平方厘米.求BD的长.
如图:三角形ABC是直角三角形,AC是圆的半径且AC=10cm.阴影Y的面积比阴影X的面积小32平方厘米.求BD的长. (2012?中山市模拟)如图,三角形ABC是面积为46.8平方厘米的等边三角形,ABCD是平行四边形,圆的半径是6厘米,求阴影部分的面积.
(2012?中山市模拟)如图,三角形ABC是面积为46.8平方厘米的等边三角形,ABCD是平行四边形,圆的半径是6厘米,求阴影部分的面积. (2012?福州)如图:三角形ABC是等腰直角三角形,直角边为4厘米,求阴影部分面积.
(2012?福州)如图:三角形ABC是等腰直角三角形,直角边为4厘米,求阴影部分面积.
 如图,三角形ABC是一个等腰三角形,AC=BC,已知∠ACD=130°,
如图,三角形ABC是一个等腰三角形,AC=BC,已知∠ACD=130°,