题目内容
 直角三角形ABC的三边分别为AC=3,AB=1.8,BC=2.4,ED垂直于AC,且ED=1,正方形的BFEG边长是
直角三角形ABC的三边分别为AC=3,AB=1.8,BC=2.4,ED垂直于AC,且ED=1,正方形的BFEG边长是| 11 |
| 35 |
| 11 |
| 35 |
分析:如图所示,连接AE、BE、CE,则S△ABC=S△ABE+S△BCE+S△CAE=
×AB×EF+
×BC×EG+
×CA×ED;
因为AB、BC、CA的长度已知,EF=EG=ED,从而可以求出EF,即正方形的边长.

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因为AB、BC、CA的长度已知,EF=EG=ED,从而可以求出EF,即正方形的边长.

解答:解:设正方形BFEG的边长为x,
则S△ABC=S△ABE+S△BCE+S△CAE,
×1.8×2.4=
×AB×EF+
×BC×EG+
×CA×ED;
2.16=
×1.8×x+
×2.4×x+
×3×1,
2.16=0.9x+1.2x+1.5,
2.1x=0.66.
x=
.
答:正方形的BFEG边长是
.
故答案为:
.
则S△ABC=S△ABE+S△BCE+S△CAE,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
2.16=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
2.16=0.9x+1.2x+1.5,
2.1x=0.66.
x=
| 11 |
| 35 |
答:正方形的BFEG边长是
| 11 |
| 35 |
故答案为:
| 11 |
| 35 |
点评:解决此题的关键是连接AE、BE、CE,利用等积转换,将三角形ABC的面积转换成含有正方形边长的等式,从而求得正方形的边长.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
一个直角三角形ABC的三个顶点的位置分别是:A点(2,4)B点( )C点(5,2).
| A、(4,5) | B、(2,2) | C、(5,4) |
 (2011?郑州模拟)直角三角形ABC的三条边分别是5cm,3cm和4cm,将它的直角边AC对折到斜边AB上,使AC 与AD重合,如图,则图中阴影部分(未重叠部分)的面积是多少cm2?
(2011?郑州模拟)直角三角形ABC的三条边分别是5cm,3cm和4cm,将它的直角边AC对折到斜边AB上,使AC 与AD重合,如图,则图中阴影部分(未重叠部分)的面积是多少cm2?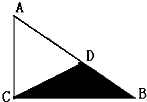 直角三角形ABC的三条边分别是5厘米、3厘米、4厘米,将它的直角边AC对折到斜边AB上,使AC与AD重合,如图,则阴影部分的面积是
直角三角形ABC的三条边分别是5厘米、3厘米、4厘米,将它的直角边AC对折到斜边AB上,使AC与AD重合,如图,则阴影部分的面积是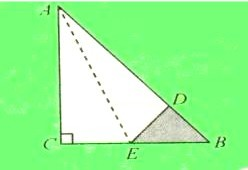 直角三角形ABC的三条边分别是5cm,3cm和4cm,将它的直角边AC对折到斜边AB上,使AC 与AD重合,如图,则图中阴影部分(未重叠部分)的面积是多少cm2?
直角三角形ABC的三条边分别是5cm,3cm和4cm,将它的直角边AC对折到斜边AB上,使AC 与AD重合,如图,则图中阴影部分(未重叠部分)的面积是多少cm2?