题目内容
 如图所示,O为圆心,三角形AOB为等腰直角三角形,它的面积是40cm2.求阴影部分的面积(π取3.14).
如图所示,O为圆心,三角形AOB为等腰直角三角形,它的面积是40cm2.求阴影部分的面积(π取3.14).分析:如下图所示,连接OC,则OC为圆的半径,且由等腰直角三角形的性质可知,AB是OC的2倍.由此可设圆半径为rcm,则OC=rcm,AB=2rcm,由三角形的面积可求得圆面积,然后用三角形的面积减去圆的面积的
即可.

| 1 |
| 4 |

解答:解:设圆半径为rcm,则OC=rcm,AB=2rcm.
×r×2r=40
r2=40,
所以圆的面积是:πr2=3.14×40=125.6(cm2),
所以阴影部分的面积是:
40-
×125.6
=40-31.4
=8.6(cm2);
答:阴影部分的面积是8.6cm2.
| 1 |
| 2 |
r2=40,
所以圆的面积是:πr2=3.14×40=125.6(cm2),
所以阴影部分的面积是:
40-
| 1 |
| 4 |
=40-31.4
=8.6(cm2);
答:阴影部分的面积是8.6cm2.
点评:本题考查组合图形的面积,解决的关键是由三角形的面积求得圆的面积.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目

 如图所示,O为圆心,三角形ABC的面积是45平方厘米.阴影部分的面积是
如图所示,O为圆心,三角形ABC的面积是45平方厘米.阴影部分的面积是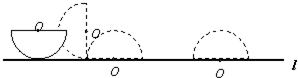
 如图所示,O为圆心,三角形ABC的面积是45平方厘米.阴影部分的面积是________平方厘米.
如图所示,O为圆心,三角形ABC的面积是45平方厘米.阴影部分的面积是________平方厘米.